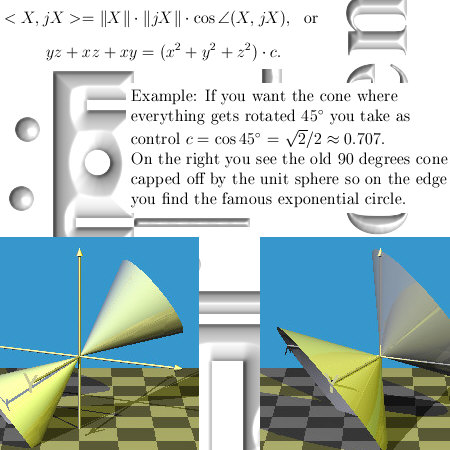
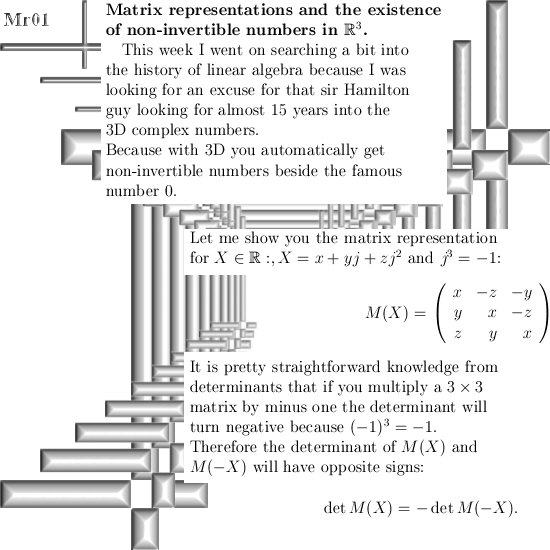
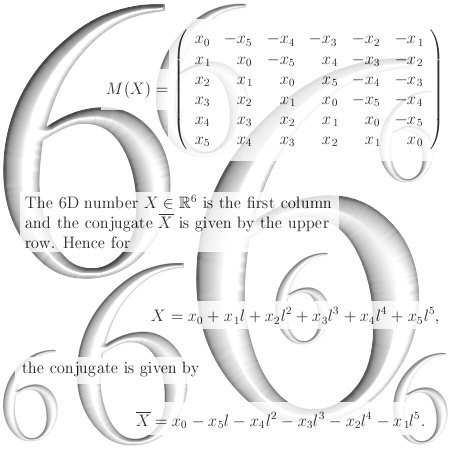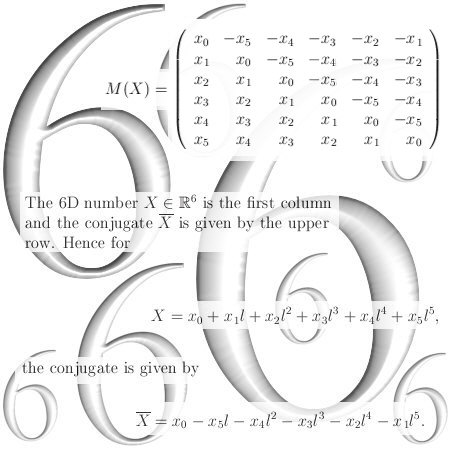This post contains seven examples of the differential operator named curl. The motivation for this update lies in the fact that after my humble opinion inside the set of equations known as the Maxwell equations there is a tiny fault: Rather likely electrons carry at least a net magnetic charge.
And because they carry net magnetic charge they not only accelerated by electrical fields but also magnetic field.
If you have an old television set with one of those fancy tubes that contain one electron cannon for a black & white television and three electron cannons for a color television. With the help of a stack of these strong neodymium magnets it is easy to give experimental proof that the electrons indeed get accelerated… Why in the course of over one hundred years not one of the professional physics professors has done this is unknown to me; may be it is the separation of ‘theoretical professors’ versus ‘experimental ones’ a reason for this omission. May be it is the use of dogma (unproven things that live inside a belief system, in this case the belief system that magnetic monopoles do not exist).
__________
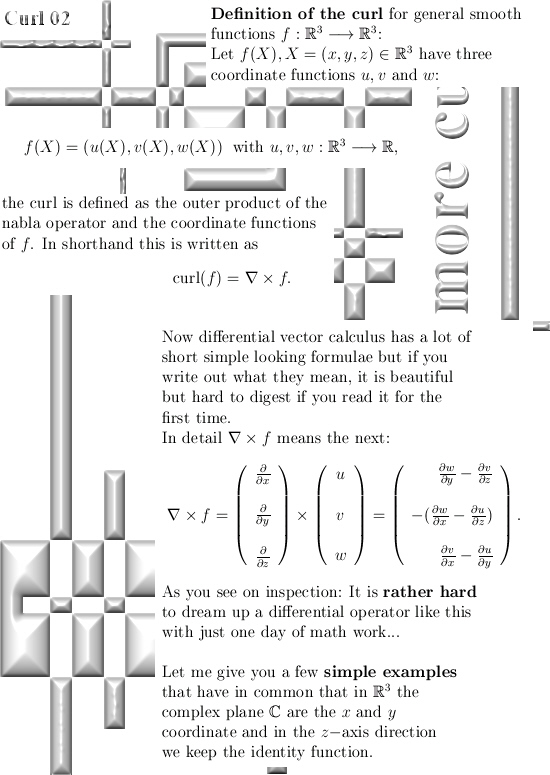
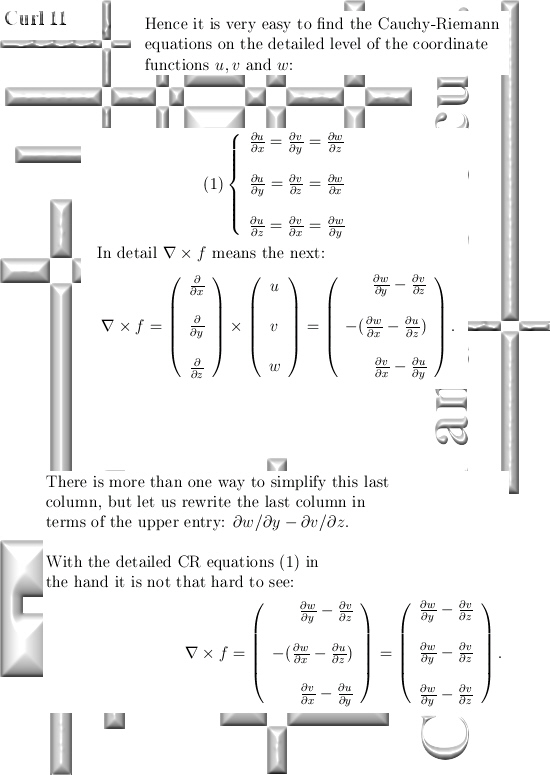
Anyway the Maxwell equations contain a lot of the curl operator, that is not needed per sé but it makes the formulae look sleek and short. Originally Maxwell had a set of like 20 equations or so while at present day only four remain. But if you see those four equations for the first time it is very impressive, only over time you get used to it.
This post is 13 pictures long, size 550 x 775 pixels.
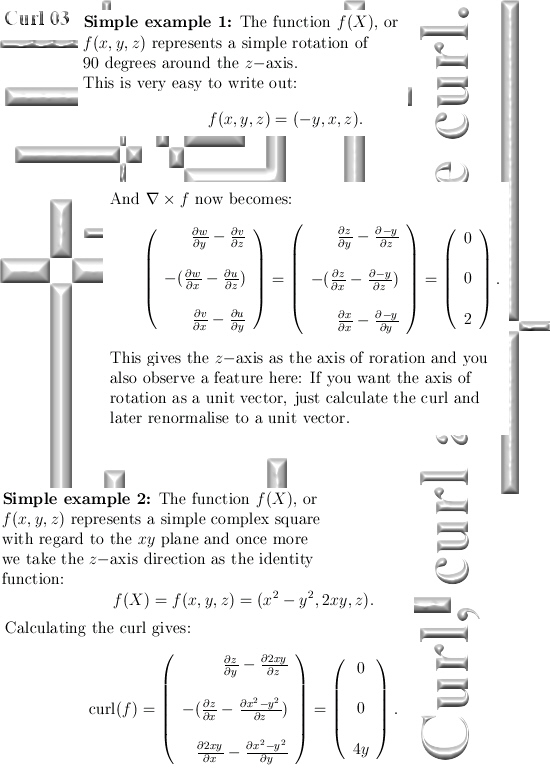
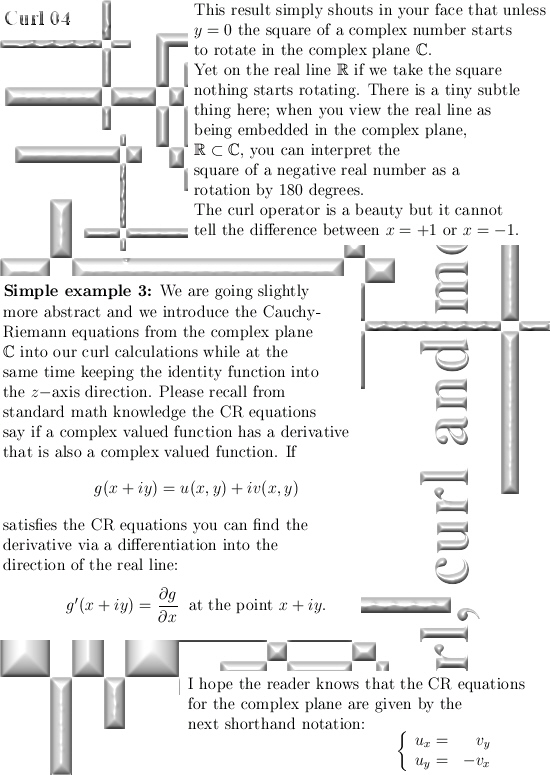
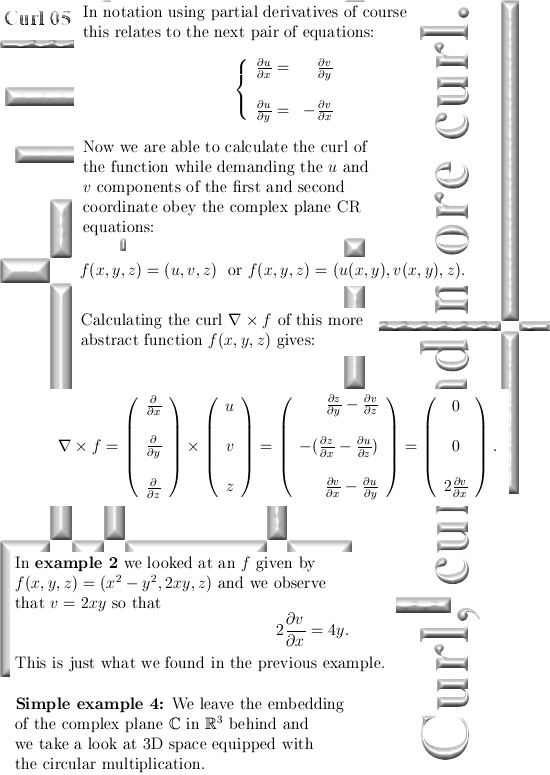
I start with examples that are as simple as possible and very slowly bring in a bit more abstraction.
Therefore I hope it is very readable, have fun with it!
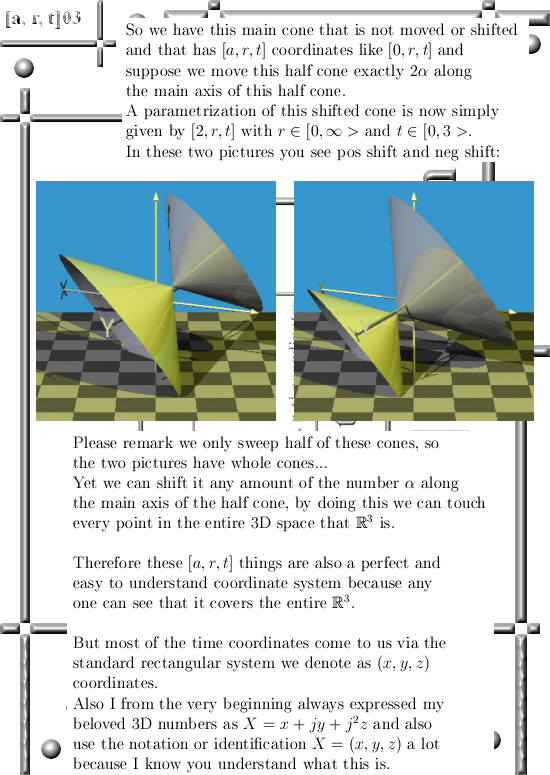
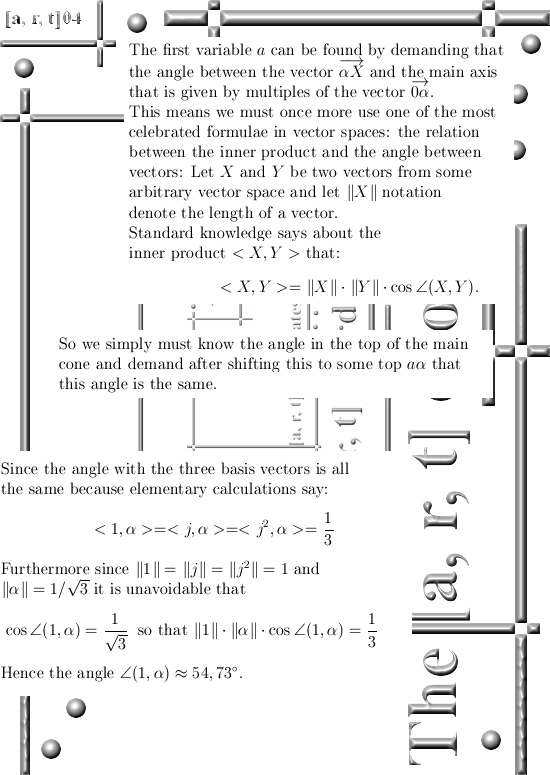
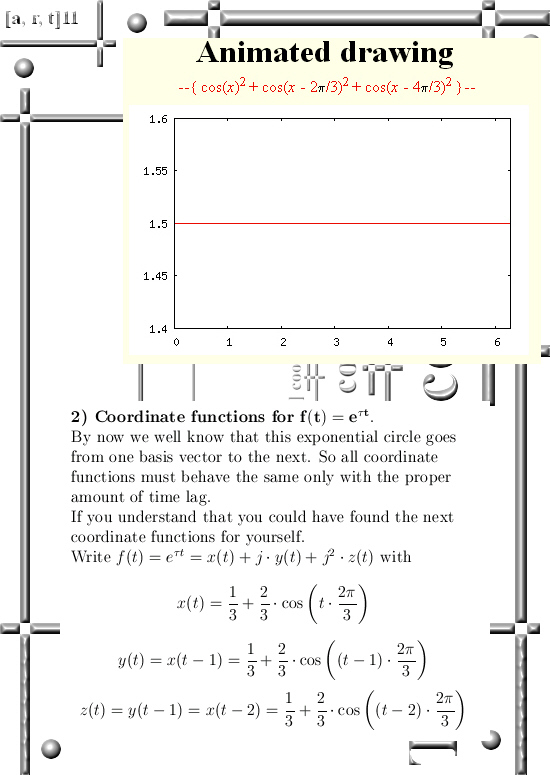
As far as I can remember, in the first year I opened these investigations into higher dimensional number systems again I calculated the curl for the complex multiplication in 3D space. In this post we only looked at the circular version of stuff.
But I can´t find it back so I cannot place a hyperlink to it.
Anyway, here is a nice wiki with the curl expressed as an integral (often much harder to calculate but nice to observe it can also be done that way):
Curl (mathematics)
https://en.wikipedia.org/wiki/Curl_(mathematics)
And because this post was motivated by all that curl in the Maxwell equations, I tried to find back when I originally started writing about electrons having magnetic charge instead of being magnetic dipoles like they are tiny bar magnets. It was 29 April that inside the math pages I found the first update on that. Here it is:
From 29 April 2014 : Do electrons have spin?
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#29April2014
Ok, that was it. Till updates my dear reader.