The so called ‘spin flip’ in atomic hydrogen is relatively important in astronomy. There is a tiny difference in energy levels of the electron in atomic hydrogen, when the spins of the nucleus and electron are the same it is said to be in the higher energy level. And with opposite spins the lower energy level is there. The difference between the two energy levels is such that a photon has a wavelength of 21 cm if this energy is released by a hydrogen atom when it’s ‘spin flips’.
In astronomy the study of this 21 cm wavelength is rather important; in our galaxy there is so much dust and clouds of all kinds of material that a lot of the visible light is blocked. But using the 21 cm radiation astronomers were able to prove the existance of the invisible spirals of our galaxy. So understanding a bit more about how the spin in atomic hydrogen flips could be important you might think.
It is not much of a secret that about 100% of physics professors think that the magnetic properties of say an electron or a proton are bipolar. So each and every electron and proton in our universe has a north and a south pole, that is the so called ‘tiny magnet’ model for elementary particles.
It is also not much of a secret that for over five years I am thinking the professors are all crazy because that bipolar stuff is just not logical on all kinds of levels. I think all electrons and protons carry magnetic charge just like they carry electric charge.
In this post we are going to take a detailed look as what happens when in atomic hydrogen the electron goes round and round the proton that is the nucleus and how the energy levels behave. As usual, if you follow that standard knowledge of bipolar ‘tiny magnets’ magnetism you only find a big mountain of total nonsense.
My choice went for atomic hydrogen because that is the most simple atom there is and by using elementary logic there is only one orbit for the electron that could explain the 21 cm wavelength as observed in astronomy.
If it is true that magnetism is always a ‘tiny magnet’ when it comes to elementary particles, in that case it is very hard to explain why the frequency emitted is precise 21 cm and nothing else. We will do a very simple thought experiment and from that we can conclude that there is only one orbit possible that gives always the 21 cm radiation.
These kind of very small energy level differences are known as hyperfine spectral shifts. They also occure in large molecules, that is why I did choose atomic hydrogen because if the explanation fails there it should also fail in large molecules. With ‘failure’ I mean the bipolar idea’s of magnetism that the professional physics professors have all of the time.
I wrote seven pictures about the energy levels in atomic hydrogen, if you base it on electrons and protons being bipolar magnets instantly you run into all kinds of trouble. After these seven pictures I show you a few video’s that make clear that 100% of professional physics people simply do not have a clue what electron spin is. As such they have a tendency to talk out of their neck, that means what they say is not thought through in any meaningful manner. Here we go:


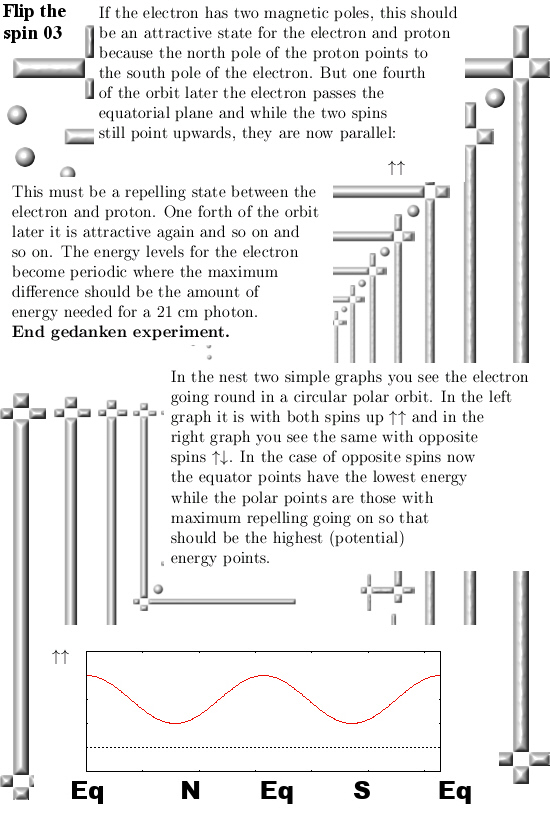
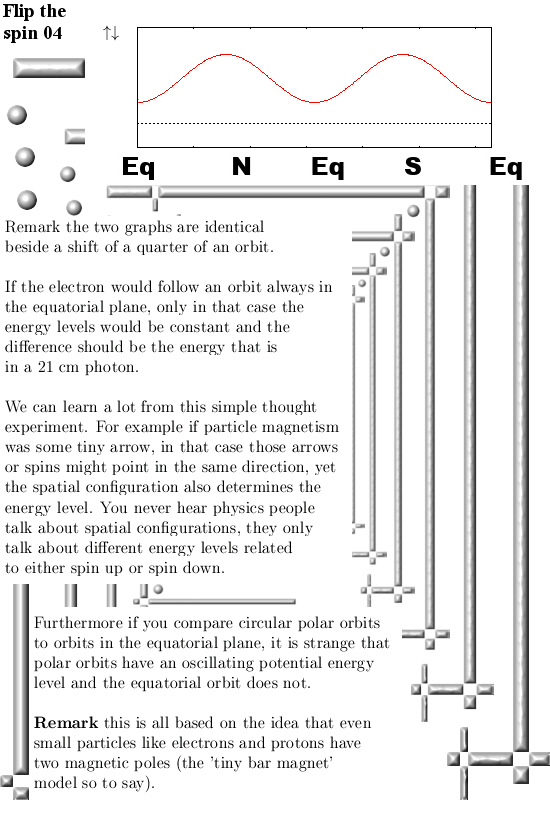
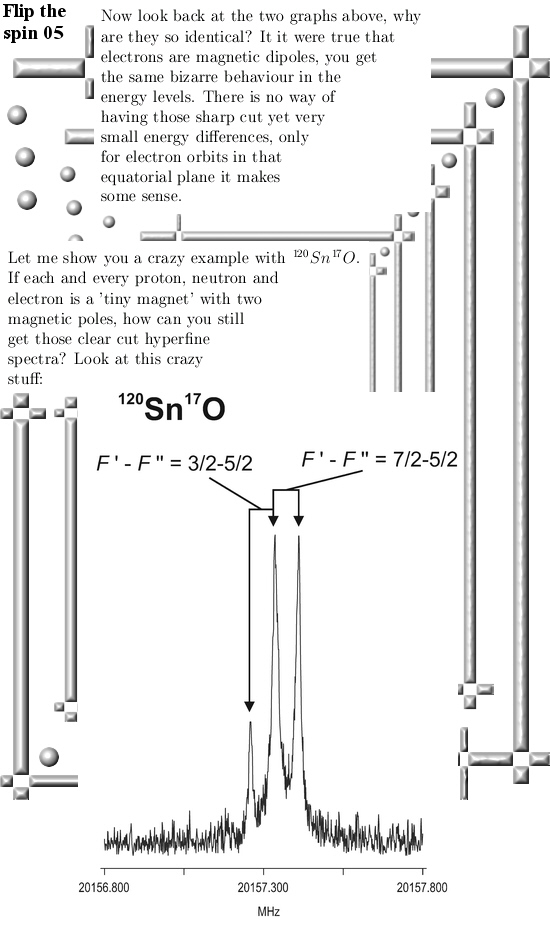

In my view the conclusions are clear: All reasoning based on electrons and protons having two magnetic poles always leads to nonsense fast. Just like here where we found orbits that have the same oscillating energy levels for both spin directions. Of course that is 100% nonsense.
This is about the sixth year I am researching electron spin. If now I do an internet search about “How to flip electron spin” and I hardly get any results I know instantly that likely it is not possible to flip the magnetism of an electron. Do such an internet search for yourself, nowhere is there any person that can explain how you can do that.
It is time for the video’s about this subject. Here is the first video, it does not contain hundreds of faults only a few minor ones like the Zeeman effect is not interaction between the electron and it’s orbit.
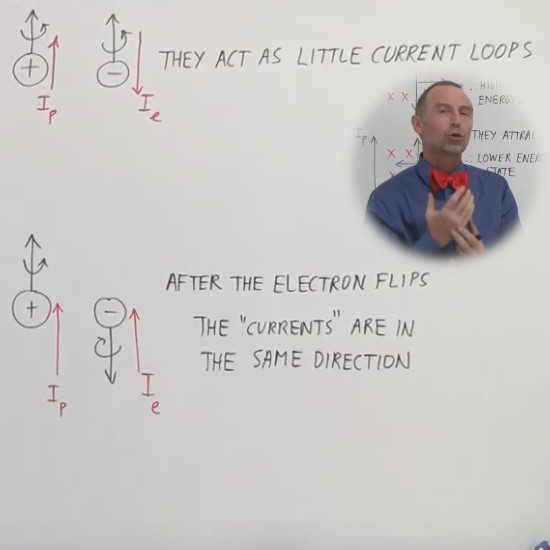
The guy from the video (Michel van Biezen) has an amazing 737K subscribers, so he makes plenty of money via the Youtube advertising scheme I just guess. In the next video you can observe the full “talking out of their neck” habit that so many physics people have. Michel tries to explain why there is an energy difference between the spin states in atomic hydrogen. He just talks from his neck by ‘explaining’ this as two currents that are repelling or atracting (like in the old experiments from the Ampere guy in the 19-th century). View it as comedy and not something serious:
I even made a screen shot from the last video. It can serve as a fundamental proof that on average physics people are very good at talking out of their neck. How you can see this as some good explanation is beyond me. At best it is comedy, at worst you understand why I will never ever try to publish something in a ‘professional journal’. These people they are all idiots and imbeciles.
Another very funny detail that often comes along when you figured out that electrons are likely magnetic monopoles is the lack of magnetic monopoles there is in our present universe according to overpaid physics professors. In astronomy they figured out that in the beginning of our universe there should have been an awful lot of magnetic monopoles. Well yes that is true, every electron is one of those things. But the overpaid idiots and imbeciles known as physics professors think otherwise and if you think electrons and protons and even quarks are always magnetic dipoles, you have a hard time finding the missing magnetic monopoles. That is why these people, retarded as they are, claim that it ‘is enough’ there is only one magnetic monopole in an entire galaxy and ‘therefore they are that hard to find’. It is another form of comedy: where are all the missing magnetic monopoles???

At last a few words on that TOE (theory of everything) and GUT (grand unifying theory) stuff: If only one detail like understanding electron spin is wrong, automatically the entire GUT or TOE will be wrong.
But yet, as I am in the sixth year of investigations into electron spin, the physics community still does not find it nessecary to prove their stupid claims on electron spin via any experiment whatsoever. Is there ever done an experiment that proves electrons have two magnetic poles? Nope! Have they any plans in doing so? Nope!
All in all I am expecting no different behavior is say the next six years: The only thing that will not be different is that physics people will keep on talking from their neck without realizing how stupid they are.