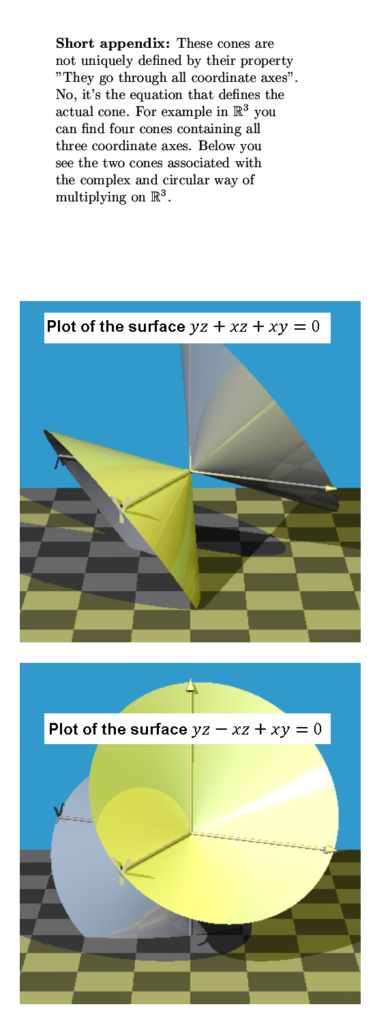
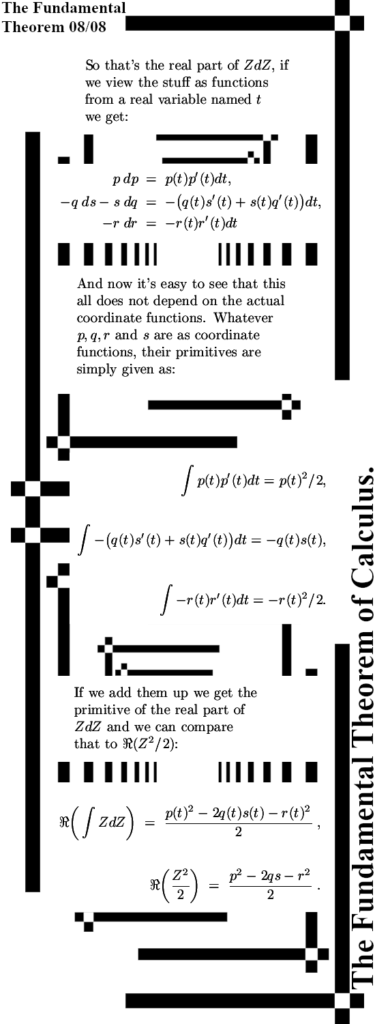
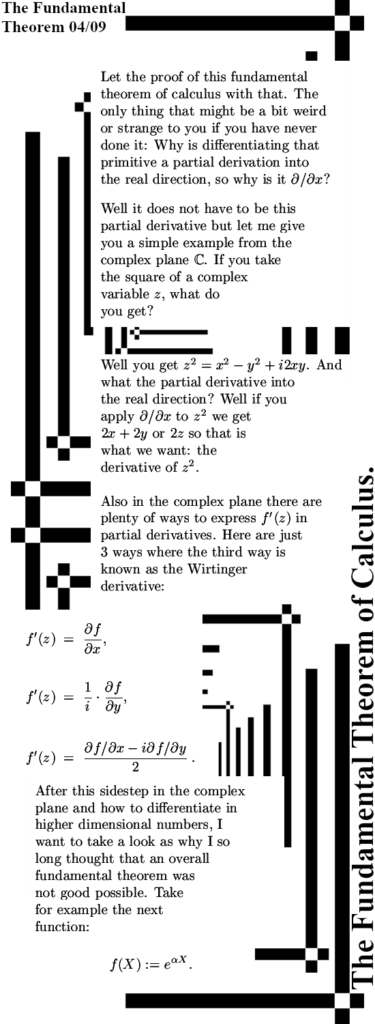
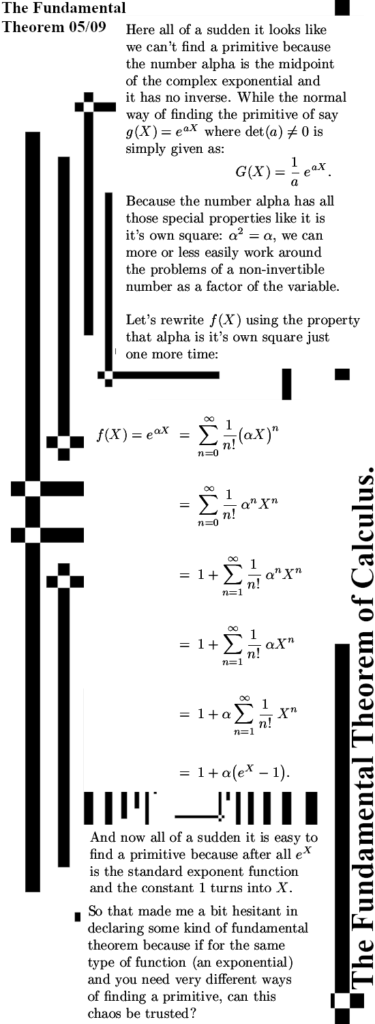
To focus the mind and or for new readers; I am of the opinion that electrons are magnetic monopoles and that their magnetic properties are just as the electric properties: permanent and monopole.
Well that is very different from the official version of electron magnetism that involves the Gauss law of magnetism that says magnetic monopoles do not exist and as such the electron must have two magnetic poles. There are a plentitude of what I name weird energy problems with bipolar electron magnetism. For example what makes an electron anti-align with an applied external magnetic field? If you look at it that way, it is easy to find much more weird energy problems and the main example I always use is the electron pair. For example molecular hydrogen is has one bonding electron pair and it’s spins must be opposite or anti-aligned as the wording goes.
Well, what explains that this is the lowest energy state? And how can H2 be stable with a magnetic configuration like this? Bar magnets are only stable and in a state of low potential energy if their magnetic fields are aligned, so why is it opposite with the two electrons in an electron pair?
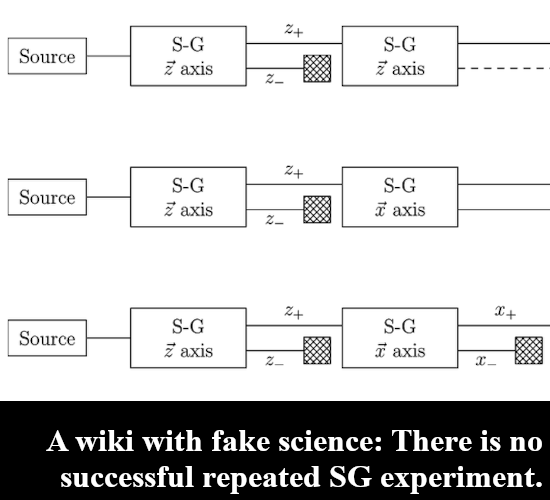
If you view electrons as having a monopole magnetic charge, you never run into those problems that are always skipped when in experimental results electron magnetism plays a role. It is just always skipped, look at any explanation of the Stern-Gerlach experiment and you never see it explained as why electrons anti-align with the applied vertical magnetic field.
But lets go to the video: Fermilab’s Don Lincoln explains how an entangled electron pair should behave. Of course he does not have any experimental evidence to back up all the stuff he claims. For 10 years now starting back since 2015 I have been searching for a repeated Stern-Gerlach experiment but there is only talking out of the neck and no results anywhere. Now a repeated SG experiment is just applying differently oriented magnetic fields to an electron and the official theory says that the probability for spin up or down is the cosine of half the angle of the difference in ortientation of the two succesive magnetic fields. So it looks a lot like linear polarization of photons only there you have the entire angle and not half the angle.
Since I became interested in electron magnetism 10 years ago I have seen a few hundred video’s on all kinds of stuff related to electron spin. Also those long video’s of say one hour or longer where researchers explain what they are doing. And often in those presentations there are some theoretical curves and with litle dots or squares the experimental results are given to the audience.
So what Don Lincoln is doing in the video is rather misleading; the curves is just the square of a cosine but there are no experimental results as far as I know.
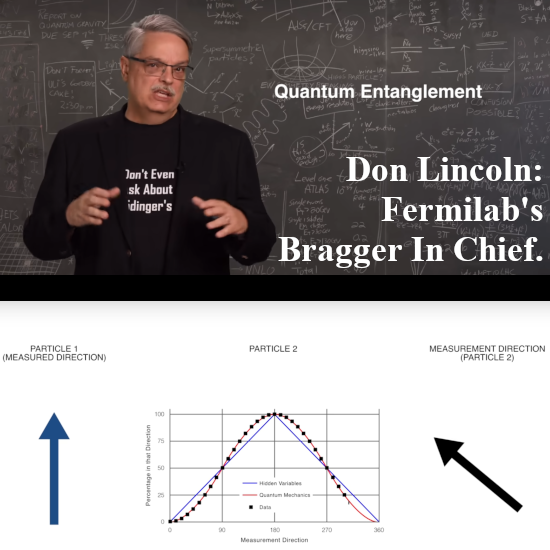
I think it was two years back or so that a few Nobel prizes were handed out and one of the recievers Alain Aspect remarked in a video that is was just to hard to do this experiment with real spin half particles like electrons. As such Alain did his experiments with photons. Don Lincoln even shows a picture of Alain and because most physics people always talk out of their neck when it comes to electron spin, he does the entanglement thing with electrons. In this video he does not brag that physics is a so called ‘five sigma’ science where all stuff is validated rigidly.
So here is the video in case you are interested in that so called non-locality stuff:
Ok, I have more to do today so let me close this short post on the ususal nonsense of official electron spin.