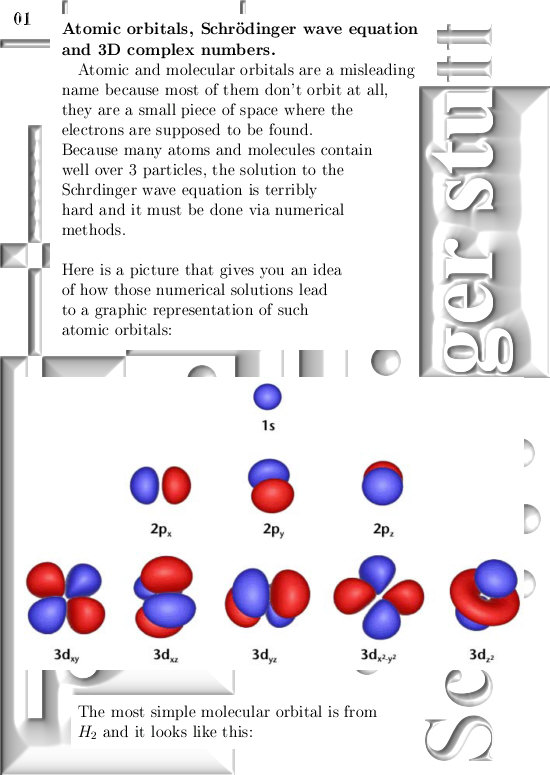
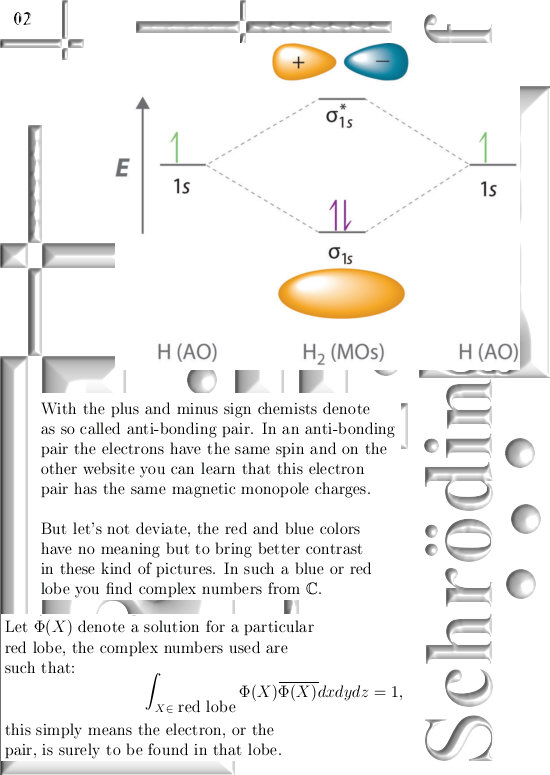
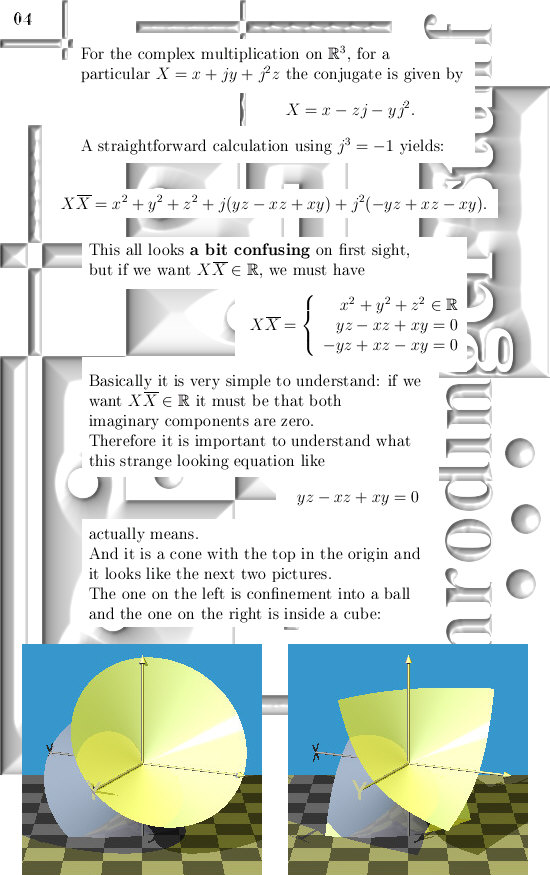
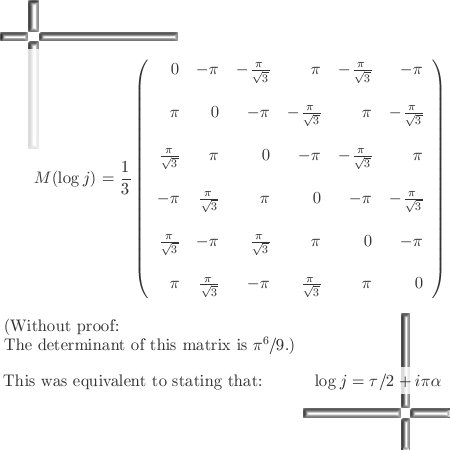
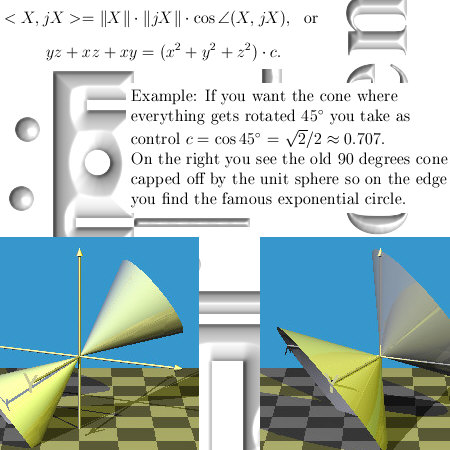
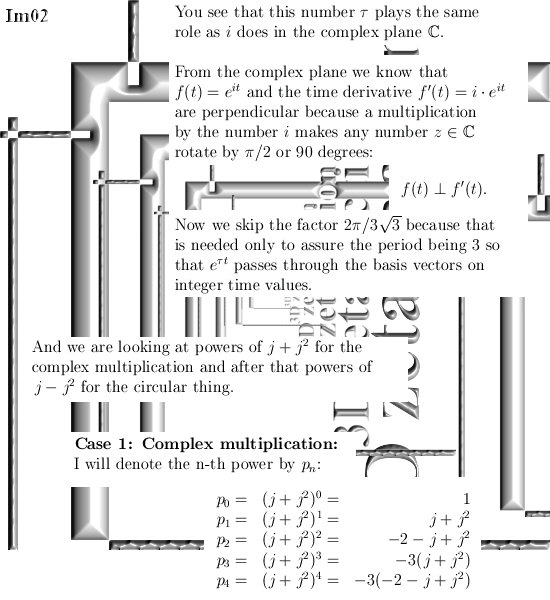
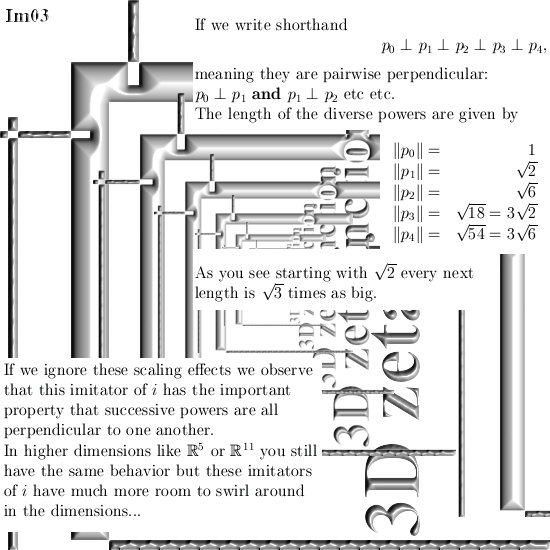
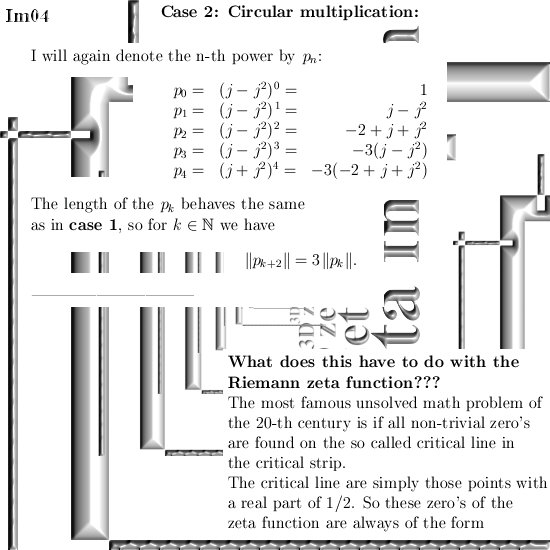
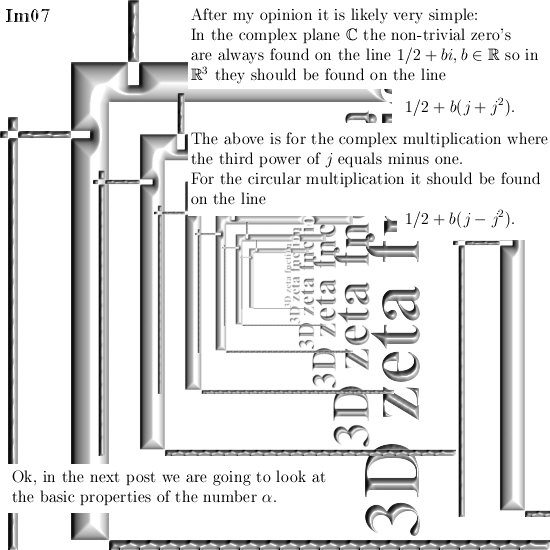
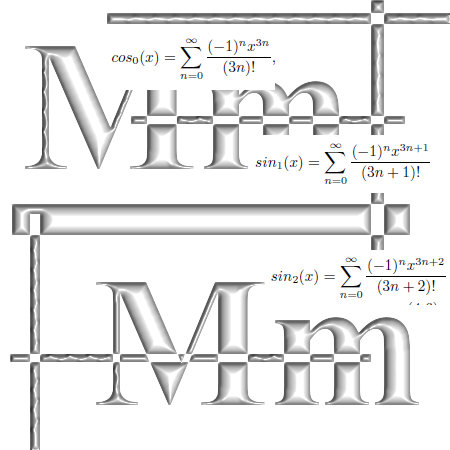
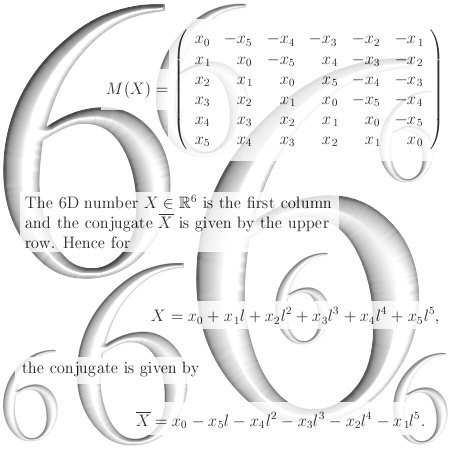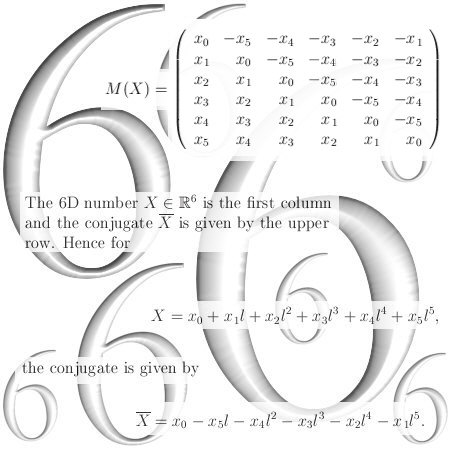Schrödinger wave equation part 2.

April 1, 20163D complex numbers, Laplacian, Quantum mechanicsReinkoVenema

A few posts back I wrote a bit about the Schrödinger wave equation related to calculating atomic and molecular orbitals for electrons using 3D complex numbers.

What I said was basically correct but also an over-simplification of the situation.
The problem is very very basic: in the 3D number system, let it be complex or circular, you just cannot solve and equation like $X^2 = -1$.
Hence the number i from the complex plane with i^2 = -1 just does not live in 3D real space.

So using alternative number systems outside the complex plane is not a straightforward thing to do, yet in principle all higher dimensional complex numbers should give the same results.
If not there would be a very basic problem inside the wave equation from quantum mechanics and I am not aware of any faults in that detail of the quantum theory.

Here are two pictures that serve as an addendum on the previous post on the Schrödinger equation:

Now if you are reading this it is very likely that at least once in your life you have seen a solution to the Schrödinger wave equation like the ‘particle in a box’. And that is not a 3D box but the one dimensional box or just an interval of the real line.

Solving the Schródinger stuff for atomic and molecular orbitals is a very different kind of game; these are always many particle systems where every particle influences the system and the entire system influence the individual particles.
Mathematically speaking it is a nightmare; analytical solutions are not possible they say.
It can only be solved numerically…

__________

But keep on dreaming, after all they also say decade in decade out that electrons are magnetic dipoles. There is no experimental proof for that only theoretical bla bla bla.

Let’s leave it with that. Till updates.

When did I find the first exponential circle in 3D space?

March 25, 20163D complex numbers, 5D complex numbers, Exponential circleReinkoVenema

It was in the Spring of 2013 when I was walking in a nearby park when it suddenly dawned on me that this exponential process that ran through the basis vectors (1, 0, 0), (0, 1, 0) and the z-axis unit vector (0, 0, 1) was periodic.
It could not be anything else because I was capable of calculating the logarithm of the first imaginary unit j.

I remember at first I just did not have a clue it would be a circle, I even had vague fantasies like may be it is a vibrating string where all those string physics professors talk about.

Now this evening I was just Googleing around a little bit when I came across this picture again:

It dates back to 30 May 2013 and I used this picture as a joke about how professional math professors look in my fantasy world. Within a week I found that the 3D complex periodic curve was in fact a circle.
So I had to laugh hard about my own joke once more because if I had known the 3D periodic thing would also be a circle I would have made the joke very different… Because one way or the other this picture now also represented me.

__________

You know this last week I am a bit puzzled by what the next post should be, in December 2013 I conducted a good investigation into the roots of unity related to the two exponential circles and because every body knows roots of unity it would a nice started for this website.

On the other website you can find it at the 05 Jan 2014 entry:

The song of omega reloaded
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#05Jan2013

At the time I was amazed with all the things you can do with the eigen values of the imaginary components j and j squared. From diagonalization to the roots of unity, my theory got definitely air born.

Later in January 2014 I found a new Cauchy integral formula (actually two just like I found two sets of roots of unity each for the admissable forms of 3D multiplication). Also in Jan 2014 I cracked the problem of 5D complex numbers.

By all standards, as far as I can see it; the two months Dec & Jan in that time were the most productive ever.

__________

Now, almost 3 years later finally stuff on Google take off, for example if this day I start searching for the phrase 3dcomplexnumbers it returns back three results from this new website.
Just look at the next screen shot picture:

So after waiting all these years, finally I begins to look as if stuff starts getting air born on some bigger scale than before.

Ok, end of this update. As usual till updates!

Just a background picture plus some bla bla bla.

March 21, 2016UncategorizedReinkoVenema

About 10 days ago I took a look at how much pictures I have crafted since the beginning of this website and I decided to take a nice holiday.

So in this update no hardcore math or softcore math, I want to show you just a background picture and talk a bit about that. Here is the picture:

For the human brain if you see things of similar shape but one is smaller compared to the other, most of the time the thing that looks small has a greater distance from where you are.
Of course there are deviations from this: When you see a child standing before a grown up you simply observe a small person standing before a larger one.

Now look carefully at the picture above, constantly the larger things are beyond those one layer smaller and constantly if it is one layer smaller it looks like the lean on the larger one.

It was years ago that by accident I found this kind of stuff, for myself speaking it looks beautiful because it transports your brain instantly into two directions:

The smaller things should be further away &
The smaller things lean on the larger ones so they should be closer…

So this gives a nice discrapency in the brain of the reader, what vision will prevail or will there be some circular insight like a cat trying to catch it’s own tail?

__________

In another development I crafted reason number 24 as why electrons and stuff like that are the long sougth magnetic monopoles, here is a teaser picture for that (click on it to land on the other website on the page about magnetic stuff):

Ok, that was more or less what I had to say today.
Till updates.

Correction number 2 on the 6D complex numbers.

March 6, 2016CorrectionsReinkoVenema

Three months ago on 06 Dec 2015 I posted the 6D numbers update because that is the smallest space that includes both the complex plane and my own invented 3D complex numbers.

To my amazement a few days ago I typed in on a Google search the phrase ‘3d complex numbers’ and when you search for pictures my teaser picture for that 06 Dec post was picture number 3.

So I started reading my own stuff again; why is this post so popular given the fact it has an extremely boring title???

It was only later that very likely my own goal of including stuff that is known, like the complex plane, must be some factor for readers clicking on that post so often. And after thinking about it coming back & so on & so on.

But I found another typo in that old post and that is the update for today; I show you the part that includes the typo and also show you the correction. Picture number 3 shows the teaser picture standing on rank 3 in the Google picture search.

Now you must never think you are king with search results like this, if for example you are in Brazil and type in the same search string ‘3d complex numbers’ you might very well get a very different result: Google like to ‘craft the search to the individual’ in order to maximize advertisement revenue…

Anyway, three pictures that form a correction on the 06 Dec post are below:

The above picture contains the stupid typo that says this imaginary number l is the square root of the complex plane thing i. This is plane stupid, in the next picture you see a correction±

In the third picture of this update you see the teaser picture on position number 3 in that Google picture search, don’t forget Google has a large bag of tricks to localize search results. So I as the idiot that I am might think that in spaces like Brazil or Australia you get the same results I forgot how Google makes the money:

Delivering search results accompanied by advertisements…

Ok end of this second correction on the 6D complex numbers. Till updates.

Atomic orbitals, the Schrödinger wave equation and 3D complex numbers.

February 29, 20163D complex numbers, Exponential circle, Laplacian, Quantum mechanicsReinkoVenema

The numerical use of three dimensional complex numbers is almost the same as the situation on the complex plane. This is caused by the simple fact that only on the main cone that includes the three coordinate axes, we have that if you multiply a number X by it’s conjugate, the result is a real number.

In the complex plane this is valid for all numbers in the plane but in higher dimensional complex number systems the situation is different; you must always pick numbers from that main cone where also the exponential circle lives (in 3D) or exponential curves (in higher dimensions).

This update is 5 pictures long, size pics = 550 by 775.

__________

One hour later:

Shit! There is a serious problem with uploading the pictures, they get uploaded but they are not visible… So you must wait at least one day longer because I do not understand the problem at hand…

Till updates.

__________

Problem with the jgp pictures is solved; according to my webhost provider it was caused by the name Schrödinger because that contains an o with two dots: ö.
My computer can handle filenames with ö so for me they looked normal but the server that hosts this website cannot deal with these kinds of symbols…

Anyway after a few days here are the pictures:

Well I am happy this strange problem of invisible pictures has been solved. Till updates.

A new type of Cauchy integral formula.

February 28, 20163D complex numbers, Exponential circle, Exponential curves, Matrix representationReinkoVenema

Yesterday I wrote a new post on the Schrödinger equation using 3D complex numbers but before I post that let’s go a bit more hardcore with a brand new Cauchy integral formula.
Actually it is not that brand new because on 18 Jan 2014 I posted it on the other website.

Now in a normal world a brand new Cauchy integral would be greeted with a lot of joy and plenty of discussion, yet that has not happened by now. Once more we observe that among professional math professors there is a severe problem concerning the so called ‘competence question’.
Or may be it is better to frame this into a lack of competence; if you have that you are also not able to judge new results properly and this is what we observe year in year out.

But I have to admit it is a relatively hardcore update, it is 10 pages long and I remember clearly it was fun to write because I wanted to prove the Cauchy formula in this way for a long time.

Source: http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#18Jan2014

__________

Now a person that is not 100% insane might wonder how the hell you calculate the determinant of a six by six matrix because in parctice that is an awful amount of work. But I used an internet applet and as such got a numerical value like about 106,821 and within a few seconds I recognized this as being pi to the power of six divided by nine.

Once back in the year 1992 I came across that number and it was kinda weird to observe that in 2014 it was still floating around in my brain. Sometimes I wonder if I am the crazy one and the math professors are the ones with healthy brains…;)

Ok, till updates my dear reader.

The Cone Theorem.

February 22, 20163D complex numbers, Exponential circle, Matrix representationReinkoVenema

On the other website I just posted 12 pages about the cone theorem. This theorem states that cones with a central axis the line through 0 and the number alpha and with their top in 0, undergo a fixed rotation when multiplied by one of the imaginary numbers like j or j^2.

You can find that on page four covering stuff posted this year.

It is important to remark I got the idea to study this particular detail because of the article in the preprint archive from Shlomo Jacobi. Now this Shlomo guy seems to be dead so I have to be a bit cautious. Let’s say these 12 pages are the way should study stuff like this & don’t forget I got the idea from this Jacobi guy while the professional math professors as usual contribute nothing.

In the next teaser picture you see how it works, while calculating some inner product you get this equation and if you fill in some allowed number for the control c you get the desired cone.

These cones are online easily made with an applet named Polyray. The great advantage of this applet is that you can fill in implicit equations so you are not bonded by some explicit stuff like

z = bla bla formulae in x and y.

You can click on the picture to land on the new update (open in a new window):

In another development I posted a few more reasons as why electrons are magnetic monopoles in the magnetic page on the other website. Now lately some folks from MIT have run six simulations of nuclear plasma and the results nicely confirm my insights in the behavior of nuclear plasma.

The MIT folks thought that in a nuclear fusion reactor you could simply neglect the contributions from the electrons because their mass is so small compared to the mass of protons and higher isotopes of atomic hydrogen. But ha ha ha, when electrons are magnetic monopoles such thinking is shallow & hollow. Anyway to make a long story short: the simulations point to a magnetic monopole electron.

Problem is I do not know how they model the plasma in detail, don’t forget the weirdo’s from the universities think electrons are magnetic dipoles and if you think that how can you make a reliable model of plasma anyway???

Here is the link around magnetic monopole stuff:
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm#17Feb2016

Enough of the bla bla bla, may be in the next post on this website I am going to dive into stuff related to the Schrödinger equation. Or something else like thousands and thousands of new and previously unknown trigoniometric identities…

We’ll see, till updates.

Seven properties of the number alpha.

February 9, 20163D complex numbers, Laplacian, Matrix representationReinkoVenema

The number alpha is one of my best finds in the field of mathematics. In all kinds of strange ways it connects very different parts of math to one another, for example when it comes to partial differential equations the number alpha plays a crucial role in transforming this of a pile of difficult stuff into something that lives in only one dimension.

You can also use the number alpha for perpendicular projections, you can use it for this and you can use it for that.

__________

Now in the previous post I told you I would write out some of the elementary properties of the number alpha, but when I finished it the thing was about 5 A4 size pages long and that would be about 10 pictures on this new website.

That would be a bit too long and also I had written nothing in the page for 2016 on the other website. So I decided to hang those five A4 pages in the old website and you get a few teaser pictures on this new website.

Here are the three teaser pictures, click on any to land on the alpha update:

The applet I used is a very helpfull tool, you can find it here:
http://calculator.vhex.net/calculator/linear-algebra/matrix-exponential-using-the-pade-approximation

Ok, that was it. Till updates and do not forget to floss your brain a bit every now and then…

Imitators of the complex number i and how this relates to the zero’s of the Riemann zeta function in 3D.

February 4, 20163D complex numbersReinkoVenema

The zero’s of the Riemann zeta function is one the things I will never be able to find because I hate it to write computer code. Always my original enthousiasm fades away quickly and after some time I simply stop working in that direction and foces on things that I like more.

Just like a few posts back when I finally decided to skip the stupid Mandelbrot fractal in three dimenstions. Computers are nice things to build but programming has never been my cup of tea let alone my pint of beer. (I am also a hobby brewer, it is a great hobby and it saves you a lot of money. The more you brew the more money you save…).

Ok in this update we are going to take a look at imitators of the number i from the complex plane. I think that most readers here already know that multiplication by i rotates everything 90 degrees. In 3D space we have similar things but not all higher dimensional number spaces contain the number i from the complex plane. In that case we must use substitutes like what I name the ‘imitators of i‘.

This update is seven pictures long, each picture is 550 by 550 pixels:

In the next post we will flea through the elementary properties of the number alpha, look at the dynamics on the line through zero and alpha (just like on the real line) and so on and so on.
Till updates.

Calculating the Laplacian using the Cauchy-Riemann equations.

January 30, 20163D complex numbers, CR equations, LaplacianReinkoVenema

Without doubt the Laplacian is a very important differential operator. It plays a major role in for example the classical wave equation and also the Schrödinger wave equation from quantum mechanics.

Now scroll a bit back until you find the post on the Cauchy-Riemann equations, at the end I used the phrase ‘Cauchy-Riemann equations chain rule style’ and this is how we can crack in a very easy way how the Laplacian operates on functions that obey the CR equations on 3D complex numbers.

I have hundreds and hundreds of pages of math stuff on the 3D complex number system and very often I use the number alpha. This number alpha is so important, not only in 3D, that it is worth to post a few posts on them.

For the time being, I just conducted a simple Google search on the phrase ‘3d complex numbers’ in the search detail for pictures. And every time this old teaser picture from the other website pops up:

At the end you see that (1, -1, 1), well that is three times alpha.

It is a nice exercise to prove that the square of alpha equals alpha.
So alpha is in the same category as for example numbers like 0 and 1 because if you square those you also get the original number back in return.

After all one squared equals one and zero squared equals zero.

End of this update, till updates.

3Dcomplexnumbers

Math as you have never seen before…

Schrödinger wave equation part 2.

When did I find the first exponential circle in 3D space?

Just a background picture plus some bla bla bla.

Correction number 2 on the 6D complex numbers.

Atomic orbitals, the Schrödinger wave equation and 3D complex numbers.

A new type of Cauchy integral formula.

The Cone Theorem.

Seven properties of the number alpha.

Imitators of the complex number i and how this relates to the zero’s of the Riemann zeta function in 3D.

Calculating the Laplacian using the Cauchy-Riemann equations.