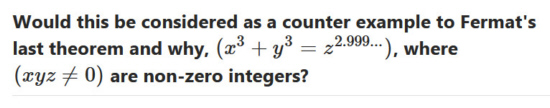Category Archives: Last Fermat theorem

Oversight of all counter examples (until now) to the last theorem of Fermat.

Last Fermat theorem

Once more I estimated my writer skills too positive; I thought it takes only 7 to 8 pictures to pen down all counter examples to the last theorem of Pierre de Fermat. But I had to stop because this post already is 10 pictures long. I organized the stuff around so called ‘levels’ so we have Level zero counter examples (the most basic ones) to level four counter examples (the most complicated ones) to the last theorem of Fermat.
We are now almost half a year further down the timeline since I looked at that video of Andrew Wiles and while looking at that video I already constructed the first counter example to the last theorem. And now we are about half a year further I have arrived at the conclusion that inside the math community there are no accepted counter examples known or discussed or whatever what they do with it. So I am not expecting my counter examples will find the place they more or less should have, acting as an adult is never within reach of the math professors.
Likely if you (as a math student or so) show these counter examples to one of your math professors, it might be it gets instantly rejected because ‘this is modulo calculus’ and has ‘nothing to do with the last theorem’. But in a pdf from Gerhard Frey (the guy from the Frey elleptic curve) I came across the next hilarious screen shot:

This is hilarious; Modulo arithmetic is allowed?????

Of course people like Andrew Wiles or Gerhard Frey will never ever react; they are perfumed princes and those high nobility people do not mingle with the plebs, farmers and peasants.
Does the absence of counter examples on the internet indicate that the math hot shots also have an absence of counter examples in their holy brain tissue? It looks like it, of course it is very well possible plenty of people found those counter examples in the past but they got only a fresh dose of what I experience for say 30 years: You get one 100% neglected all of the time. After all if you are an outsider like me, the collective of math professionals acts very much like a secretive incest club. Those kind of clubs are not very open to communication with the outside world. Not that math professors are pedophiles but the behavior is keeping things inside is very much the same.
An interesting question is if perfumed prince Andrew Wiles knows these counter examples. My guesstimate is no. And why is that? After the pictures of the main post I will show you that video from the Abel prize lecture and there you can see Andrew formulating the last theorem of Pierre de Fermat. He does it more or less in the following manner:

For integers x, y and z with xyz not equal to 0, it is impossible that
x^n + y^n = z^n. This for integers n > 2.

If Andrew would have knowledge in his brain about these counter examples likely he would have formulated it like this:

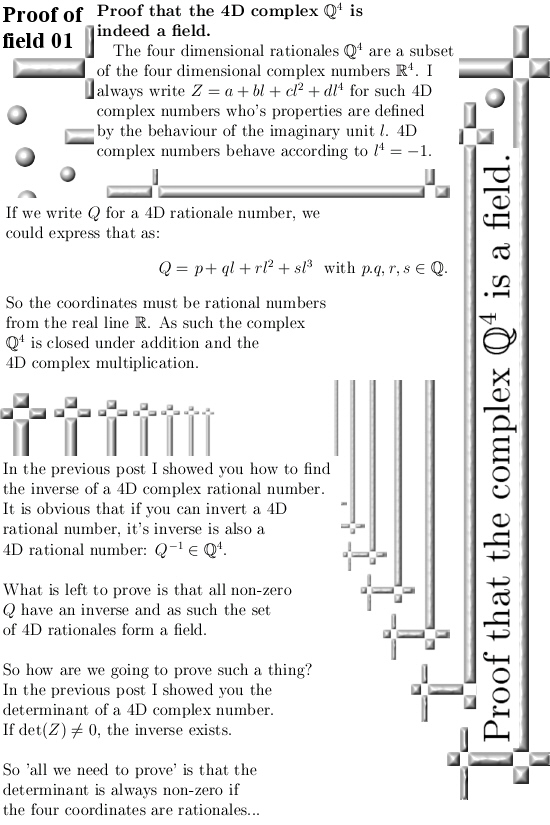
For positive non-zero integers x, y and z, it is impossible that
x^n + y^n = z^n. This for integers n > 2.

All counter examples I found in the last five months have the property that xyz = 0 because say the x and the y form a pair of so called divisors of zero. (The level zero counter examples do not have this property, but I did not find the level zero examples myself…) Now it could be that Andrew is as evil as he is smart and formulated it with the xyz not zero way in order to subtlelly exclude my wild math adventures. But in reality it is much more likely that Andrew is just another perfumed Princeton professor. So my estimate is and stays that Andrew is not aware of the rather simple counter examples to the last theorem of Pierre de Fermat as found below…

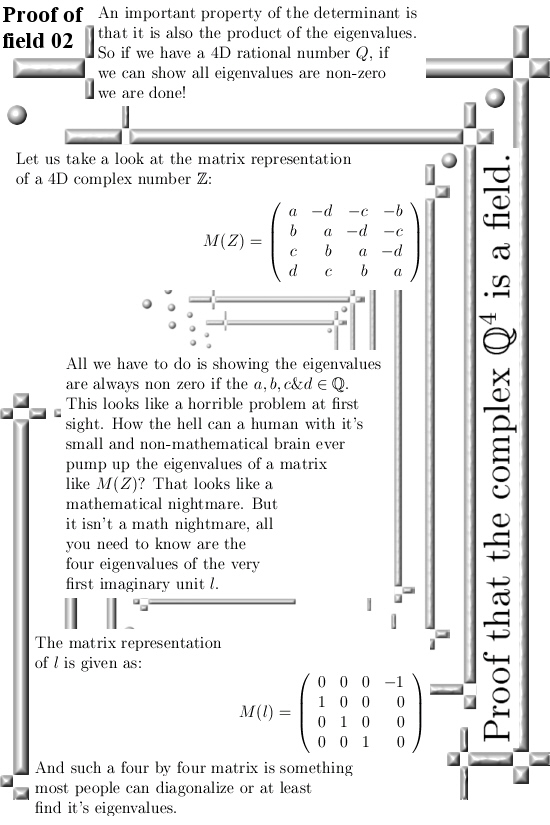
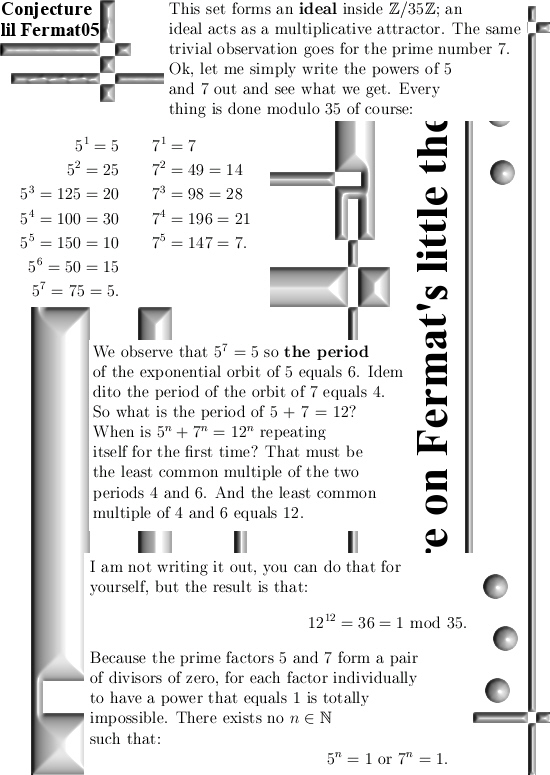
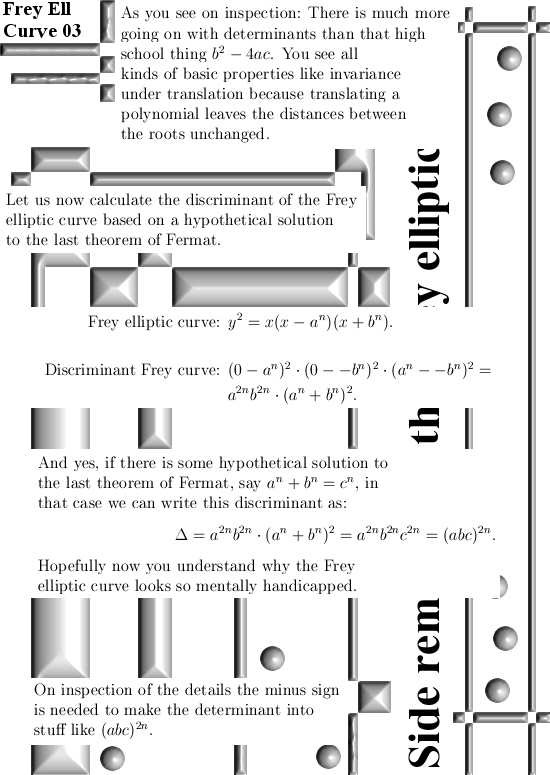
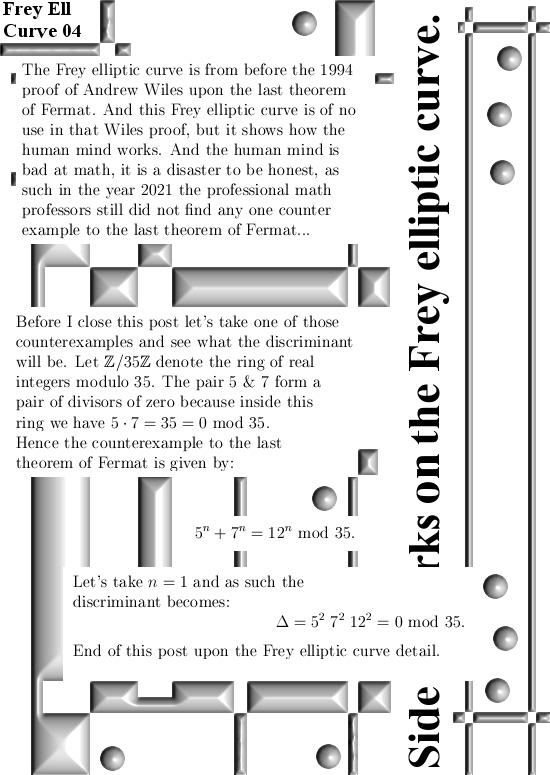
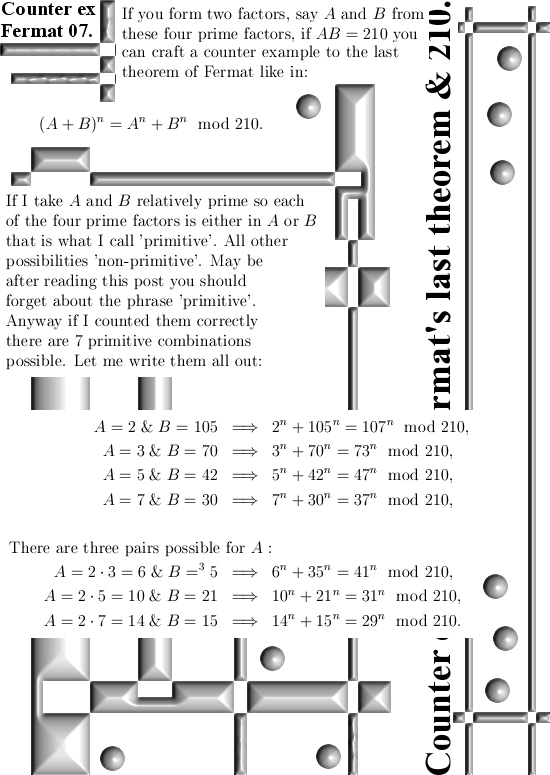
Ok, this post is 10 pictures long and it only contains the stuff found that is based on modular arithmetic. In my view it is all rather basic and as such should explain itself. The main basis is that ‘divisor of zero’ stuff where two non zero numbers multiply to zero. For example if we take the real integers modulo 35, in that case if we multiply 5*7 we get 0 because 35 = 0 inside the ring of integers modulo 35. It’s all so basic that it makes you wonder once more: why is this not inside the math classes on universities? But for that answer you must ask the perfumed professors and the perfumed professors never answer because they are much more busy of getting a fresh stack of perfume. That’s life…
Have fun reading it

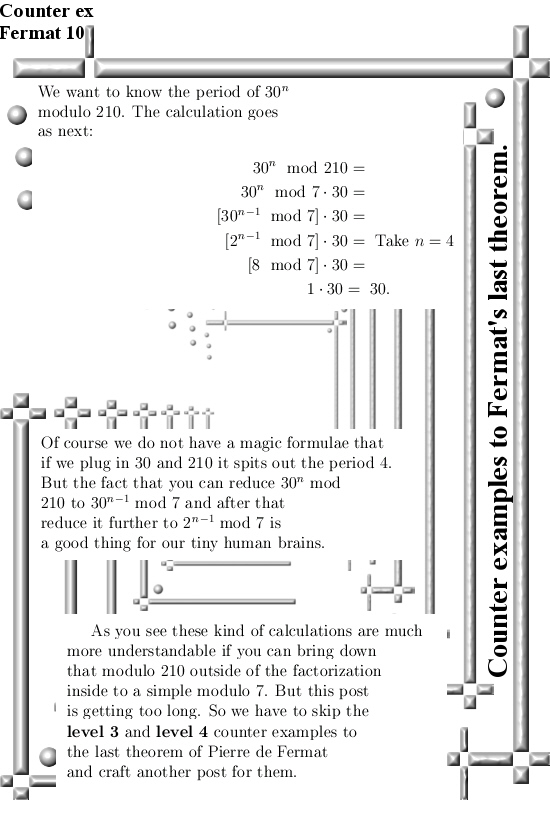
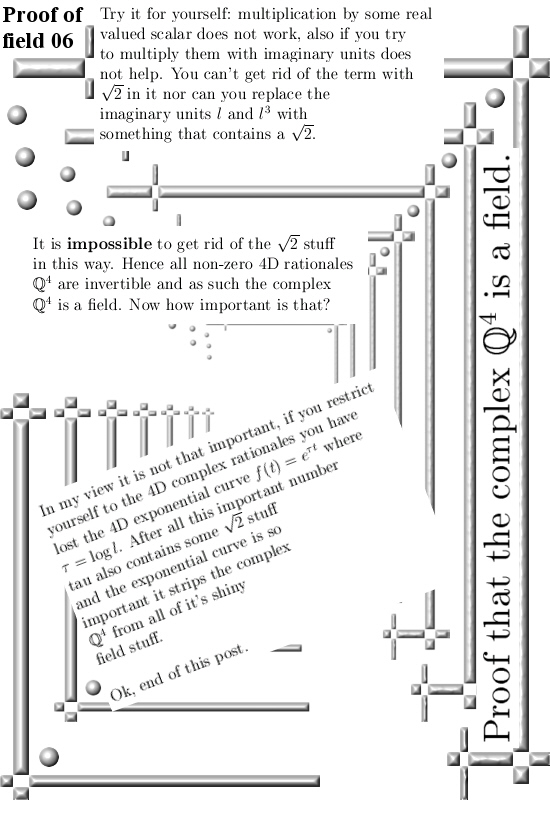
For me the only thing I learned while writing this post is that you can use that simple rule for writing 30^n mod 210 in stuff mod 7. It is the same kind of calculation as in the modified little theorem of Fermat and this is also a detail I could not find on the internet.
Oh yes now I am in a laughing mood: Can we prove the perfumed professors are indeed perfumed overpaid people? Yes we can: They will also not react of the modified or improved little theorem of Fermat. We will need a few years of time for that, but why should they react?

Ok, I promised you the video of a Princeton perfumed prince named Andrew Wiles, here it is and please pay attention to the way he formulates the present day formulation of the last theorem of Pierre de Fermat:

At only one minute into the video we observe that likely Andrew has no clue whatsoever about the above counter examples to the last theorem of Pierre de Fermat:

Why this way of formulating the problem?

End of this post. Thanks for your long lasting interest in these details on the last theorem of Pierre de Fermat.

Two things and a proof that the 4D complex rationales form a field.

4D complex numbers, Exponential circle, Last Fermat theorem, Matrix representation

I finished the proof that was originally meant to be an appendix to the previous post. And I have two more or less small things I want to share with you so lets get started with the first thing:

Thing 1: Tibees comes up with a very cute program of graphing 3D surfaces. It’s name is surfer, the software is very simple to use and it has the giant benefit of making graphs from implicit equations like
f(x, y, z) = 0. For example if you want the unit sphere in 3D space you must do x^2 + y^2 + z^2 – 1 = 0. Now for this website I always used an internet applet that uses ray tracing and by doing so over the years such graphs always look the same. But this surfer program has cute output too and it has the benefit you don’t need to be online. Here is how such a graph looks, it is the determinant in the space of 3D complex numbers, to be precise it shows the numbers with a determinant of 1:

By the way, the surface of this graph is a multiplicative group on it’s own in 3D space. I never do much group stuff but if you want it, here you have it. And for no reason at all I used GIMP to make one of those cubes from the above graph. It serves no reason beside looking cute:

The Tibees female had a video out last week where she discusses a lot of such surfaces in three dimensional space using that surfer software. And she is a pleasant thing to look at, it is not you are looking at all those extravert males drowning in self-importance only lamentating shallow thoughts. The problem posed in the video is an iteresting one, I don’t have a clue how to solve it. Title of the video: The Shape No One Thought was Possible. It is a funny title because if you start thinking about all the things that math professors thought were not possible you can wonder if there is enough paper in the entire universe to write that all out..
Link to the Surfer program in case you want to download & install it:
https://www.imaginary.org/program/surfer.

So far for thing 1.

Thing 2: The last weeks it is more and more dawning on me that all those centuries those idiots (the math professors) did not find counter examples to the last theorem of Fermat. Nor was there any improvement on the little theorem of Fermat. Only Euler did some stuff on the little theorem with his totient function, but for the rest it is not much…
Well since Jan of this year I found many counter example to the last theorem of Fermat and in my view I made a serious improvement on the little theorem of Fermat.
So is the improvement serious or not?
Here is a picture that shows the change:

So it’s modulo ap instead of modulo p.

On a wiki with a lot of proofs for the little theorem of Fermat they start with a so called ‘simplification’. The simplification says that you must pick the number a between 0 and p. So if you have an odd prime, say a = 113, does the little theorem only make sense for exponents above 113?
And can’t we say anything about let’s say the square 113^2?

With the new version of the little theorem we don’t have such problems any longer. Here is a screen shot from the start of that wiki, the upper part shows you the improvement:

Here is a link to that wiki that is interesting anyway.

If you follow that link you can also scroll down to the bottom of the wiki where you can find the notes they used. It is an impressive list of names like Dirichlet, André Weil, Hardy & Wright and so on and so on. All I want to remark is that non of them found counter examples to the last theorem nor did they improve on the little theorem of Fermat. Now I don’t want to be negative on Dirichlet because without his kernel I could never have crafted my modified Dirichlet kernel that is more or less the biggest math result I ever found. But the rest of these people it is just another batch of overpaid non performers. It’s just an opinion so you don’t have to agree with it, but why do so many people get boatloads of money while they contribute not that much?

End of thing 2.

Now we are finally ready to post the main dish in this post: the proof that the subset of four dimensional rational numbers form a field. Math professors always think it is ‘very important’ if something is a field while in my life I was never impressed that much by it. And now I am thinking about it a few weeks more, the less impressed I get by this new field of four dimensional complex numbers.
Inside the theory of higher dimensional complex numbers the concept of ‘imitators of i‘ is important: these are higher dimensional numbers that if you square them they have at least some of the properties of the number i from the complex plane. They rotate everything by 90 degrees or even better they actually square to minus one.
Well one of the imitators of i in the space of 4D complex number is dependent of the square root of 2. As such it is not a 4D rational complex number. That detail alone severely downsizes my enthousiasm.
But anyway, the next pictures are also a repeat of old important knowledge like the eigenvalue functions. Instead of always trying to get the eigenvalues from some 4×4 matrix, with the eigenvalue functions with two fingers in your nose you can pump out the eigenvalues you need fast. This post is six pictures long each size 550×825 pixels.
Here we go:

Yes that is the end of this post that like always grew longer than expected. If you haven’t fallen asleep by now, thanks for your attention and don’t forget to hunt the math professors until they are all dead! Well may be that is not a good idea, but never forget they are too stupid to improve on the little Fermat theorem and of course we will hear nothing from that line of the profession…

Inverses for the field of 4D complex rationales.

4D complex numbers, Last Fermat theorem, Matrix representation

This year starting in January I found more and more counter examples to the last theorem of Fermat. As a by product when we looked at the stuff on the 4D complex numbers, we found that if we restrict ourselves to the 4D rationales, they were always invertible. And as such they form a field, this is a surprising result because the official knowledge is that the only possible 4D number system are the quaternions from Hamilton. So how this relates to those stupid theorems of Hurwitz and Fröbenius about higher dimensional complex numbers is something I haven’t studied yet. But that Hurwitz thing is based on some quadratic form so likely he missed this new field of 4D complex rationales because the 4D complex numbers are ruled by a 4 dimensional thing namely the fourth power of the first imaginary unit equals minus one: l^4 = -1.
Compare that to the complex plane that has all of it’s properties related to that defining equation i^2 = -1.

And because we now have a 4D field I thought like let’s repeat how you find the inverse of a 4D complex rational number. And also prove that we have a field as basic a proof can be. But while writing this post I had to abandon the second thing otherwise this post would grow too long. Of course in the past I have crafted a post for finding the non-invertible 4D complex numbers but in that post I never remarked that rational 4D complex numbers are always invertible. To be honest in the past it has never dawned on me that it was a field, for me this is not extremely important but for the professional math people it is.

When back in Jan of this year I found the first counter example to the last theorem of Fermat I was a bit hesitant to post it because it was so easy to find for me. But now four months further down the time line I only found two examples where other people use some form of my idea’s around those counter examples and both persons have no clue whatsoever that they are looking at a counter example to the last theorem of Fermat. But in a pdf from Gerhard Frey (that is the Frey from the Frey elliptic curve that plays an important role in the proof to the last theorem of Fermat by Andrew Wiles) it was stated as:
(X + Y)^p = X^p + Y^p modulo p.
That’s all those professionals have, it is of a devastating minimal content but at least it is something that you could classify as a rudimentary counter example to the last theorem of Fermat. It only works when your exponent if precisely that prime number p and it lacks the mathematical beauty that for example we have in expressions like:
12^n = 5^n + 7^n modulo 35.

Anyway this post contains nothing new but there is some value in repeating how to find inverses of higher dimensional complex numbers. All you need is a ton of linear algebra and for that let me finish this intro on a positive note: Without the professional math professors crafting linear algebra in the past, at present day for me it would be much harder to make progress in higher dimensional complex numbers. And it is amazing: Why is linear algebra relatively good while in higher dimensional number systems we only look at a rather weird collection of idea’s?
This post is made up of seven pictures each of size 550×800 pixels.

Stupid typo: Z = 1 + l +… so the real part must be one.

Ok ok this post is not loaded with all kinds of deep math results. But if you have a properly functioning brain you will have plenty of paths to explore. And the professional math professors? Well those overpaid weirdo’s will keep on neglecting the good side of math and that is important too: That behavior validates they are overpaid weirdo’s…

For example the new and improved little theorem of Fermat: The overpaid weirdo’s will neglect it year in year out.
That’s the way it is, here is once more a manifestation of the new and improved little theorem of Fermat:

Let’s leave it with that. Thanks for your attention.

A second proof of the new little theorem of Monsieur Pierre de Fermat.

Last Fermat theorem

This is not a totally new proof, basically it is already part of the proof in the previous post. But I was able to write it down a bit more compact. It seems that you can skip large parts of the previous proof and still the result is standing. The stuff you can skip is not unimportant or so; it is where I compared those additive and multiplicative orbits and you really need that in order to understand a bit more of what is happening in rings like the integers modulo 35 (or any other composite number of course).
Often I name the ordinary intergers ‘real integers’. I hope that is not confusing, with a real integer I mean whole numbers as they are found on the real line. I do that do make clear the difference with the Gaussian integers as they are found in the diverse complex spaces.

Right now I am already about four months busy with this stuff that all started in January with counter examples to the last theorem of Fermat. All in all I never expected to be able to make an improvement on the little theorem of Fermat. But sometimes the old little theorem gives answers that are indeed correct but still is not that satisfactory. In the old little theorem you take some real integer a, you pick a prime number p that has no common factors with a and you know that in that case:
a^p mod p = a. But if the prime number p is relatively small, I mean a is larger, you don’t get back a but a mod p.

This post is short, only three pictures in the usual format of 550×775 pixels but I added two appendices so all in all there are five pictures in this post. In the second appendix I show you that if we square 125, the old little theorem gives back a 1 while my new version of the little theorem nicely gives back 125. Of course there is always much discussion possible of something is ‘better’ or not. It is only in the sense that also with small prime numbers you get back your a I mean it is ‘better’. One thing is clear: it is definitely more beautiful. My favorite formulation stays the formulation with two prime numbers like in:

p^q = p mod pq &
q^p = q mod pq.

The symmetry in the pair of equations above is, in my opinion, more beautiful compared to the old version of the little theorem of Fermat. At last I want to remark that I have a thing in common with Monsieur Fermat: math is a hobby for me. Now the old little theorem was improved upon by the professional professor Euler and with a little smile on my face I can say: Hey Euler did you miss the above pair of cute equations?

Yes he did, just like a guy named Einstein never had a fucking clue about electron spin. But likely that is a story for another day, in the meantime we have five pictures with the second proof of the new little theorem. Have fun reading it and never forget: If it is math, sometimes you need a few more days to figure it all out!

In a wiki upon proofs of the little Fermat theorem you can find that one of the authors did indeed find a counter example to the last theorem of Fermat. You can find it under ´Multinomial proofs´in the next link:
Proofs of Fermat´s little theorem. Link used:
https://en.wikipedia.org/wiki/Proofs_of_Fermat%27s_little_theorem

Ok, that was it for this post. Thanks for your attention.

Proof of the conjecture on Fermat’s little theorem.

Last Fermat theorem

The proof is finished and in the end it went rather different from what I expected before the writing down of this new proof. I hope the main ideas are easy to understand. I formulated the proof with a concrete example; so not two general prime number p and q. But I took p = 5 and q = 7 and as such we are calculating in the ring of integers modulo 35.
One of the key ideas is that we have so called additive orbits, for example the additive orbit of 5 is the set {0, 5, 10, 15, 20, 25, 30}. The additive orbit are just the multiples of 5, it is handy to view the above set as multiples of five and as such: {0, 5, 2*5, 3*5, 4*5, 6*5}.
On the other hand we have exponential orbits, the exponential orbit of 5 are the powers of 5 like in the next sequence: 5, 5^2, 5^3, 5^4…
An important observation is that any power of five is also a multiple of five; that means the exponential orbit is inside the additive orbit. For example 5^3 is on the exponential orbit, 5^3 = 125 = 20 modulo 35 = 4* 5.
So the number 5^3 from the exponential oribt corresponds to 4*5 on the additive orbit. The goal of the proof is to show that the period of 5 in her exponential oribt is 6 and the period of the exponential orbit of 7 is 4.
That will ensure our new little theorems of Fermat:
p^q = 5^7 = 5 modulo 35 &
q^p = 7^5 = 7 modulo 35.
Remark that powers of 5 can never be a multiple of 35 simply because any power of 5 does not contain a prime factor 7, so not all of the numbers on the additive orbit are allowed.
Another key idea is that if we reduce stuff modulo 35, this is the same as reducing stuff modulo 7 on the multiples of 5. Let me explain: Take the number 50, inside the mod 35 ring this is 15. But 50 = 10* 5 = (10 – 7)*5. I was able to pull that modulo 35 stuff on a ring back to modulo 7 stuff on a field…

Another thing I want to remark is that I formulated these new little theorems of Fermat mostly in prime numbers. That makes them more symmetric like the beautiful pair of equations above, but it can be a bit more general like I showed you in the last post using the number 210 that is made up of four different prime factors. And even that is not needed; prime factors can be double or triple it does not matter. As long as the exponent is a prime number my freshly crafted proof will sail you through all the troubles there are.

In a parallel development I found a perfect math professor. It’s a female and she has an amazing career record: At age three already a Fields medal while before she was nine years of age already the third Abel prize for lifetime achievement math… It is surely amazing…;)

Unlike other math professors, she is thinking it all through… Amazing!

But serious, this post is not that long. Only five pictures and like I said above it is not a ‘most general’ kind of proof but it uses a fixed pair of prime numbers. I think it is better this way because if I would formulate all the stuff in a general setting the only people who could understand such a writing are the ones who already figured the stuff out for themselves… Ok, all pictures are in the usual 550×775 pixelf format so here we go:

We are almost at the end: Let me give you one more example as why only in the exponent you need a prime number. We take the number 8 and raise it to the power 5 and do the reducing modulo thing by 40.
Doing so gives that: 8^5 mod 40 = 32768 mod 40 = 32768 – 819*40 = 8.

Ok, that is what I had to say for this post.

More versions of Fermat’s little theorem using the number 210.

Last Fermat theorem

A few posts back I used the number 210 to craft seven so called ‘primitive’ counter examples to the famous last theorem of Fermat. Each of those seven primitives can be changed in an infinite number of ways so we have seven streams of counter examples to the last Fermat theorem. It has to be remarked that all counter examples I found since Jan are all based on the so called divisors of zero idea. So if you hear people talking about that in a timespan of 3.5 centuries nobody was able to find counter examples, they are not lying if they mean a counter example on the space of real integers. Yet in Jan this year we observed I had two counter examples using the 3D Gaussian integers, it was one or two days later I found all those counter examples on the spaces of modulo arithmetic.
Beside his so called last theorem Fermat has done a lot more and one of those things is Fermat’s little theorem. To my surprise there are many more variants possible of this little theorem. The little theorem says that for a number a coprime to some prime number p the following holds:
a^p = a mod p. Two numbers are coprime if they share no common factor, if a is a number between 1 and p this is always the case.

The most simple example: a = 2 and p = 3. The little theorem now says that 2^3 mod 3 = 2. This is correct because the remainder of 8 divided by 3 equals 2.

The variants I found can be summarized as next:
2^3 mod 6 = 2 and
3^2 mod 6 = 3.
As you see I take it modulo a composite number. I still do not have a satisfactory proof so for the time being this is a conjecture. I am planning a seperate post for outlining where in my view the problems are that must be proved for the status of conjecture being dropped. So for the time being this is Reinko’s little conjecture.

But can you use a composite number with more than two factors? Yes but you can only use prime numbers in the exponent. Not that it will always fail if you do not use a prime exponent but that is a mathematical story for another day. Anyway this post uses the number 210 because it is the smallest number with four prime factors.
Before we go to the content of this post, to my surprise yesterday I observed a proof that is strikinly similar to the easy way I constructed those counter examples to the last theorem of Fermat. I found it on brilliant.org, here is a link:
https://brilliant.org/wiki/fermats-little-theorem/
Over there they prove the little theorem for a + 1 if it is true for a. Now why do they not use it for finding counter examples to the last theorem of Fermat? Well my dear reader, the human mind is bad at math. We are only monkeys or smart apes if you want, math is something that fascinates our minds but humans are horribly bad at math. Believe me: I am a human myself…;)
Here is a picture from that proof from brilliant dot org:

It is a bit hard to read but all those middle terms contain factors of p.
Therefore they vanish when you take the modulo p thing.

The whole post is only two pictures long, each of the ususal size of 550×775 pixels. Here we go:

Ok, that was it for this post. Thanks for your attention & see you in the next post.

A conjecture on Fermat’s little theorem.

Last Fermat theorem

To my amazement there are many more forms of the so called Fermat little theorem. Fermat’s little theorem uses numbers that are relatively prime to each other (also known as coprime numbers or better: coprime real integers). I hope it is not confusing for you that I write ‘real integers’ but that is meant to make clear these are not Gaussian integers but integers from the real line.
The little theorem of Fermat has some generalizations like the Euler theorem and a person named Carmichael also worked on stuff like that. Yet the coprime stuff is always assumed while the results I found last week do not need that at all. But I do need prime numbers in the exponent, that’s all.
When I found those counter examples to Fermat’s last theorem about 3 months back I was amazed I could find nothing of that on the entire internet. Ok my first stuff was done with 3D complex & circular Gaussian integers so that is logical nobody else writes about that. But that expressions like 5^n + 7^n = 12^n modulo 35 is something that baffled my mind. This is so simple to prove that it is hard to understand why this is not a standard counter example to the last theorem of Fermat. To refresh your mind: the last theorem of Fermat says there exists no integers such that x^n + y^n = z^n for n > 2. This has been an open problem for about 3.5 centuries of time, it was solved by Andrew Wiles in the beginning of the nineties of the last century but even Andrew never mentions those easy to craft counter examples to the last theorem of Fermat.

A paradox.
The last theorem of Fermat was unproven for centuries. But the far more easy little theorem of Fermat was proven rather quick and that proof is very easy compared to the Andrew Wiles thing. Now I am having the opposite problem: The counter examples to Fermat’s last theorem are so simple to construct that in the beginning I was hesitant to use it all. While for these new variants of the little theorem of Fermat, I do not know how to prove that. So my stuff is more or less opposite to the historical developments as they are known; that is why I consider this a little paradox.

In this post I formulate a few easy to understand variants of the little theorem of Fermat. In this post I choose to do it as symmetrical as possible like in the next pair:
7^11 = 7 modulo 77 &
11^7 = 11 modulo 77.
As you see on inspection; these are clearly variants of the little theorem but the exponents and the 77 of the modulo thing are not coprime. For myself speaking I consider the above pair as an example of ‘mathematical beauty’. Of course it is hard to give a definition of ‘math beauty’, you recognize it when you see it but it is hard to define because beauty itself is not a mathematical object or so.

Anyway beautiful or ugly as a math professor, this post is six pictures long all in the standard format of 550×775 pixels. Here we go with the picture stuff:

Typo at ‘w often looked’ should be ‘we often looked’.
Remark we are using the counter examples to the last theorem of Fermat…

A few posts back I crafted seven counter examples to the last theorem of Fermat and those were based on the number 210. Actually each of those seven ‘primitives’ gave rise to an infinite series of counter examples so that the overpaid math professors once more know their contribution to this all: ZERO!
But you can make four new little Fermat theorems using the number 210 so may be that is the next post. On the other hand the USA based Fermilab has all kinds of new results out upon the muon and they keep on thinking that elementary particles like electrons and muons are magnetic dipoles. Instead of offering some fundamental proof for the magnetic dipole nature of electrons we only get a complicated story that, as usual, neglects that electrons and muons get accelerated by magnetic fields.

So I don’t know about the next post. Well thanks for your attention, have a healthy life and ruthlessly kill all math professors. Or may be not…;)

Side remarks on the Frey elliptic curve.

Last Fermat theorem

Since this is the post number six on the Fermat stuff already, I decided to create a new category for this kind of math. It is no secret my knowledge of algebra is rather rudimentary, a lot of things in algebra are things I do not like to study or think about. I always had trouble learning algebra, often those people come up with say 15 definitions of algebra objects but all those definitions have the weight of a fly and rather soon I am lost in the forest. I much more prefer more heavy definitions of math objects (like the Cauchy-Riemann equations) and not stuff that is a semi-simple defined on a semi-simple kind of curve…
So I do not know much about number theory, a few days ago I downloaded the entire proof of Andrew Wiles where he proves that the last theorem of Fermat is actually true. Well already in the very first line I get lost; and in that proof you have all that Galois stuff so I think that I skip that entire proof for the time being.
A lot of things are weird in number theory. For example that Frey elliptic curve is based on a hypothetical solution to the Fermat equation a^n + b^n = c^n. If you interchange a and b in the Fermat thing, every thing stays the same. But you get a different elliptic curve if you interchange a and b in that Frey ellipic curve. So I just had no clue; wtf is going on here? Luckily I found a video of Gerhard Frey explaining a bit about what and why and the elliptic curve he defined is done in that way so that the discriminant can be simplified using that theoretical solution to the last Fermat theorem. So it is not crazy but it has it’s own logic, yet search for yourself: how many texts are there that speak about this Frey elliptic curve and actually tell you this? Most math writers simply repeat the (old) knowledge and are bad at explaining why stuff is such and so.

I always work alone, actually it is not work but an important hobby, and because I have to figure out every thing alone I have no access to people with a lot of knowledge on the details & the broader lines of some kind of math theory. Because I work alone this often takes more time. Yet on the universities where the people are supposed to work together they have never found 3D complex numbers or counter examples to the last Fermat theorem. In other sciences like physics it also goes like crazy if you read what they made of electron spin in 100 years of time. So working together is not a guarantee of speeding things up. On the contrary if after a full century you still think that, for example, the electrons is a magnetic dipole you are crazy to the bone.

This post is a short one, only four pictures long. I nicely work out what that discriminant is supposed to be. Likely people like Andrew Wiles and Gerhard Frey have never seen counter examples to the last theorem of Fermat, so why not at the end of my post take a look at what happens in that case? Well it does not look very promising for the collective of overpaid math professors; such a determinant of the Frey elliptic curve is always zero… Anyway on all spaces I found where we have counter examples to the last Fermat theorem, such a discriminant is always zero.
And that is regardless of the last Fermat theorem counter example being true or false; sorry Gerhard Frey I don’t think this approach will bring any fruits at all…
Well here are the four pictures, all of the standard size of 550×775 pixels.

The only reason I wrote six posts on the Fermat stuff is that those counter examples like 5^n + 7^n = 12^n modulo 35 are too cute to ignore.
End of this post, thanks for your attention.

Counter examples to the last theorem of Fermat using the number 210.

Last Fermat theorem, Uncategorized

Ok ok one more post upon the easy to find counter examples to the last theorem of Fermat. In this post we will take a look at the real integers modulo 15 and modulo 210. It still amazes me how easy it is to find counter examples to the last Fermat theorem using the integers modulo n where n has at least two prime factors. From my own education I remember that the integers modulo n are studied in math mostly via additive groups and multiplicative groups. For some strange reason it is not commonly studied via rings where you have the benefit of addition and multiplication inside one simple to understand structure of numbers… Inside professional math there is always that tendency to study fields only, of course there a legitimate reasons for that like it makes math life often more simple. But rings are not fields, rings allow for non zero numbers that are non-invertible anyway. As such you can always find plenty of pairs of so called ‘divisors of zero’ and once you have stuff like that it is always a piece of cake to find counter examples to the last theorem of Fermat.

Yet I tried a few times to find some counter examples on the internet but all I got was boatload after boatload of total nonsense like the weird stuff paraded in the previous post. Could it be that math professors tried to find counter examples to the last theorem of Fermat while they never dipped into the power of the divisors of zero? That’s crazy because the Fermat theorem was open for about 350 years. I think many people have found the easy to understand results in this post before I did but if they tried to get the stuff out they were blocked by the scientists of those days and as such in the year 2021 it is hard to find something back.

Compare it to electron spin; it is hard to swallow that I am the very first person in history that claims electrons cannot be magnetic dipoles because it is just not logical for hundreds of reasons. Yet in the daily practice of how science is done at the universities, it is a no show that electrons are magnetic monopoles. What happened to all those other persons that understood that electrons cannot be magnetic dipoles? Well at least they got neglected and university life just went on with electrons being a magnetic dipole because ‘we are so smart’ and ‘the standard model explains almost everything’. And more of that nonsense…

This post is 8 pictures long, all of the usual size of 550X775 pixels.
Since it is about counter examples to the last Fermat theorem I expect it will not make much headlines in the news for another 3500 years.
After all the only thing university people are good at is being incompetent…;)
Here we go:

At last I found a more or less readable article about near misses of the last Fermat theorem. It was found inside old work from Ramanujan so that is always interesting. Most of the time when I looked for counter example to the last Fermat theorem I only find piles of garbage but this time I tried it with Duckduckgo and something readable comes floating up:
Ramanujan surprises again.
https://plus.maths.org/content/ramanujan

Ok that was it for this post. Thanks for your attention.

Why can’t I find counter examples to Fermat’s last theorem on the internet?

3D complex numbers, Last Fermat theorem, Uncategorized

After a few weeks it is finally dawning on me that it might very well be possible that the professional math people just do not have a clue about how easy it is to find counter examples to the FLT. (FLT = Fermat’s Last Theorem.) That is hard to digest because it is so utterly simple to do and understand on those rings of integers modulo n.
But I did not search long and deep and I skipped places like the preprint archive and only used a bit of the Google thing. And if you use the Google thing of course you get more results from extravert people. That skews the results of course because for extraverts talking is much more important compared to the content of what you are talking or communicating. That is the problem with extraverts; they might be highly social but they pay a severe price for that: their thinking will always be shallow and never some stuff deeply thought through…

As far as I know rings of the integers modulo n are not studied very much. Of course the additive groups modulo n are studied and the multiplicative groups modulo n are studied but when it comes to rings all of a sudden it is silent always everywhere. And now I am looking at it myself I am surprised how much similarity there is between those kind of rings and the 3D complex & circular numbers. Of course they are very different objects of study but you can all chop them in two parts: The numbers that are invertible versus the set of non-invertibles. For example in the ring of integers modulo 15 the prime factors of 15 are 3 and 5. And those prime factors are the non-invertibles inside this ring. This has all kinds of interesting math results, for example take the (exponential) orbit of 3. That is the sequence of powers of 3 like in: 3, 3^2 = 9, 3^3 = 27 = 12 (mod 15), 3^4 = 36 = 6 (mod 15) and 3^5 = 18 = 3. As you see this orbit avoids the number 1 because if it would pass through 1 you would have found an inverse of 3 inside our ring and that is not possible because 3 is a non invertible number…

Likely my next post will be about such stuff, I am still a bit hesitant about it because it is all so utterly simple but you must never underestimate how dumb the overpaid math professors can be: Just neglecting rings modulo n could very well be a common thing over there while in the meantime they try to act as a high IQ person by stating ‘We are doing the Langlands program’ & and more of that advanced blah blah blah.
Anyway it is getting late at night so from all that nonsense weird stuff you can find on Google by searching for counter examples to the last theorem of Fermat I crafted 3 pictures. Here is the first one:

I found this retarded question on quora. For me it is hard to process what the person asking this question was actually thinking. Why would the 2.999…. be important? What is this person thinking? Does he have integer solutions to say 2.9 and 2.99 and is this person wondering what would happen if you apply those integer solutions to 2.99999999…..???????

It is retarded, or shallow, on all levels possible. So to honor the math skills of the average human let’s make a new picture of this nonsense:

We will never be intimidated by the stupidity of such questions and simply observe these are our fellow human beings. And if ok, if you are a human being running into tons of problems, in the end you can always wonder ‘Am I a problem myself because I am so stupid?’

If you have figured out that question, you are getting more solid & you look more like a little cube:

I want to end this post on a positive note: Once you understand how stupid humans are you must not view that as a negative. On the contrary, that shows there is room for improvement.