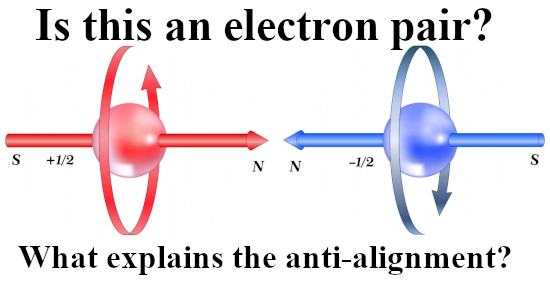
A couple of weeks back I already showed this video from Dr. Erica Carlson on the other website. I did select that video because in the second half of that video she talks about electron spin configurations that minimize the energy in stuff that is known as spin ice.
Since all those energy problems that I have with viewing electrons as bipolar tiny magnets are always skipped, I decided to use this video as a short post on magnetism. In videos like this the pattern is always the same: at the surface it all looks logical like in this video the spin configuration in that stuff known as spin ice. But video after video I have seen over the last years, always when we need to look at crazyland they always skip that. When the energy stuff gets crazy, they just skip it. Now this is absolutely not some form of a conspiracy, these people like Erica simply believe the bipolar magnetic electron is true and as such they have a blind spot into the problems: They just don’t see the problems because of their blind spot.
In the year 2015 I started to doubt that electrons were tiny magnets with two magnetic poles. I started doubting that after I tried for myself to explain the results of the so called Stern-Gerlach experiment. In my view the results were only explainable if we use magnetic monopole electrons. A few days later reading all those official explanations I understood I had to be cautious. And at the begining back in 2015 I knew nothing about electron spin, all I knew was that people from physics thought they were tiny (bipolar) magnets. It’s been a long journey from there back in 2015 and it will also be a long long journey going from our present year 2024. After all the belief that electrons are tiny macroscopic magnets is deeply rooted in 100% of the physics community.
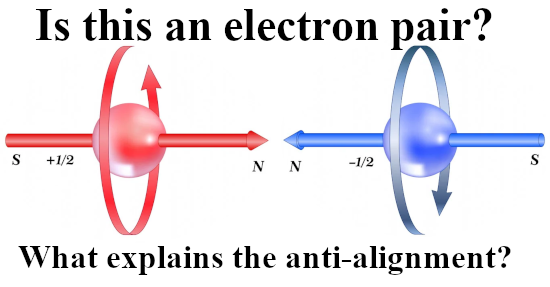
In this post, for the first time since 2015, I included a simple expression about how the professional physics professors view the potential energy of electrons related to magnetism. It is somewhere below and it is the same as we have for macroscopic magnets like say two bar magnets.
If you hold two bar magnets south to north pole, that is the minimum potential energy because it costs energy to separate them. And if you hold two bar magnets say north pole to north pole, that is the situation of high potential energy.
The post itself is four pictures and two additional figures and of course the perfect video from Dr. Erica Carlson. Say for yourself, this video is a perfect 10 with all kinds of animations I can only dream of. Ok ok, there is just one tiny tiny error in it: electrons are not tiny magnets.
But for the rest it’s a “PERFECT 10” kind of video.


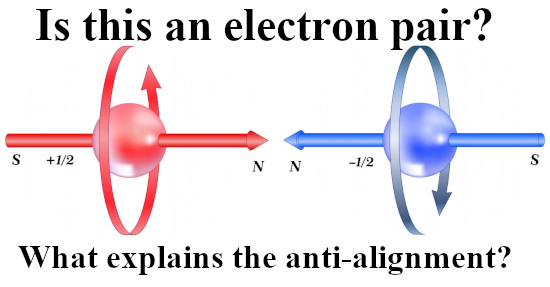

That was more or less the end of this post but I made one more picture depicting another big energy problem that the official version of electron spin has: The behavior of a single electron in an applied magnetic field.
After all if it were true that electrons are tiny magnets, if you apply a magnetic field to electrons shouldn’t they all perfectly align with that magnetic field and as such fall into their lowest potential energy state?
Yes in an ideal world they should, but we live in a world where we not only have a lot of professional physics professors but also television physics professors. And they never talk about the energy problems there are with the electron as being tiny magnets.
So this is a strange strange world where physics just ingores simple problems like the last picture of this post:

Oh yes the stability problems we have if it were true that electrons are tiny magnets. As you see in the video it is always skipped and their brains never go down that route… It is what it is and here is the video:
Lets leave it with that, the next post will be about matrix representations of conjugtes of 2D complex numbers. They are weird and also lovely now I have my new method of understanding the process of conjugation.
And as always thanks for your attention and not falling asleep before you read these last words of this post.