I didn’t plan on another ‘just a video post’ but I am still working on a new math post on the seven properties of the number alpha. All in all that is going to be one of the longest posts written, that why it takes a relatively long time. So that’s my excuse for another ‘just a video post’.
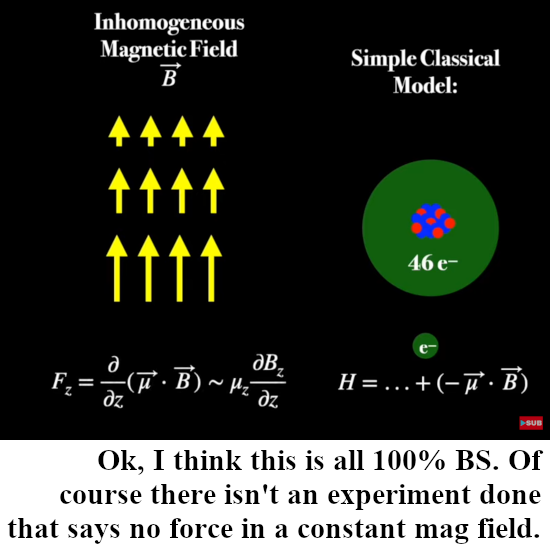
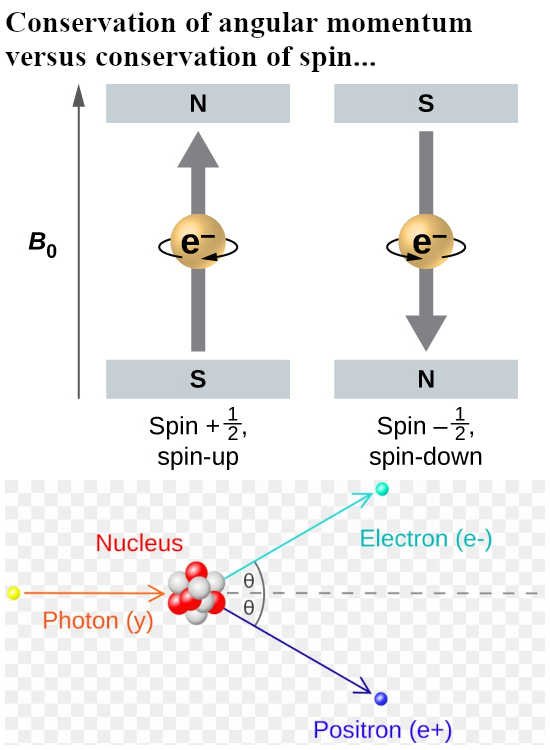
This is another video from Dr. Jorge S. Diaz and again the video is very good made with lots of interesting historical details. In it he shows what Gerlach thought before the experiment was done, that is in the first picture below. In case you did not know it: all that stuff with a varying magnetic field from strong to weak was thought out beforehand. Only the Stern Gerlach guys thought that the silver atoms themselves would act as tiny magnets. That’s why also in the simple math below you see the emphasis on the gradient of the magnetic field.
And that brings me once more to an important critisism, not on the video but on the lack of experimental proof that electrons are not accelerated in a constant magnetic field. Ok ok there is still the Lorentz force so that’s easier said then done but it is just missing. Just like there is no experimental proof or evidence that electrons are dipole magnets.

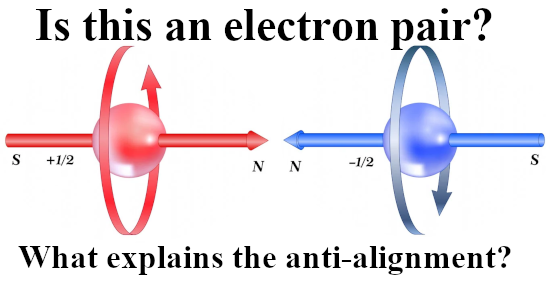
As all video’s on the Stern-Gerlach experiment this one too fails to explain as why tiny magnets would anti-align themselves with the applied magnetic field. After all this raises their potential energy and as such I consider this an important energy problem that you only have if you view electrons as tiny magnets.
I remember that back in 2015 when I myself did see this experiment for the first time, it was the fact that the silver atoms would more towards the weaker part of the magnetic field that I just could not understand. But in one or two days I had figured out that if you view electrons as magnetic monopoles, you don’t have weird problems. But back in the time I knew just nothing about electron spin so I had some learning to do.
In the video but also other sources say that it were Einstein himself and Heisenberg who pushed heave for a so called repeated or sequential SG experiment. On may occasions I have argued that such a repeated experiment has never been done in one century of time. And that is strange because if you were successful in this, you would almost one 100% sure have won a Noble prize. And that’s what all the physics people want; a Nobel prize… A repeated experiment would validate the probabilistic nature of electron spin, but it’s just not there and nobody in the physics community gives a shit about that. That’s why so often I say these people are talking out of their neck.
At about 19 minutes into the video Dr. Jorge S. Diaz claims that a repeated SG experiment has been done by Frisch and Segré but that is just plain wrong. In the Frisch-Segré experiment they tried to rotate the spin of an electron. But it failed so to bring this up as an example of a repeated SG experiment is not allowed.

Before I show you the video I want to make a quote from the pdf on the Frisch Segré experiment. The Frish and Segre guys claimed in an article to have observed nondiabetic spin flip. I doubt if that is true but at present day in a lot of physics labs they too think the can flip electron spin in say a diamond nitrogen vacency. But I think that when this happens, they have just another electron with the opposite magnetic charge.
This is a WordPress website and I believe they have a ‘quote environment’ hanging around somewhere. So lets try:
Immediately, Heisenberg and Einstein proposed multi-stage Stern–Gerlach experiments to explore deeper mysteries of directional quantization [2]. Ten years later, Phipps and Stern reported the first effort [8], which was unfortunately discontinued owing to Phipps’ involuntary return to the US [2]. A year later, Frisch and Segrè modified the same apparatus by adopting Einstein’s suggestion on the use of a single wire instead of three electromagnets to rotate spin; they also improved magnetic shielding, slit filtering, and signal detection [2]. Despite the use of three layers of magnetic shielding for the middle stage (i.e., the inner rotation chamber), the remnant or residual fringe magnetic field was still 0.42 × 10−4 T (or 0.42 G). Rather than fight the fringe magnetic field further, they took advantage of it. The magnetic field from the wire in the middle stage cancels the remnant field to produce a magnetic null point, around which the field is approximated as a magnetic quadrupole; consequently, they successfully observed nonadiabatic spin flip [9].
Well it is now high time for the video:
In my mind or in my memory the Frisch Segré experiment failed so it is good to be corrected. But all in all you really can’t say that this was a repeated Stern Gerlach experiment. It was trying to flip the spin of an electron. And that while I think the magnetic properties of electrons are just like their electric properties: permanent and monopole.
Ok that was it for this ‘just a video post’. Thanks for your attention.